单变量线性回归
symbols
m = number of training examples
x’s = “input” variable / features
y’s = “output”variable / “target” variable
(x,y) - one training example
(x^(i) , y^(i)) - the i training example ( i 表示索引,不是幂)
hypothesis(假设,机器学习术语— 输出函数)
univariate 单因素
代价函数
调整参数 最小化代价函数—– h(x)-y ,拟合数据

contour figure /plot (等高线图)
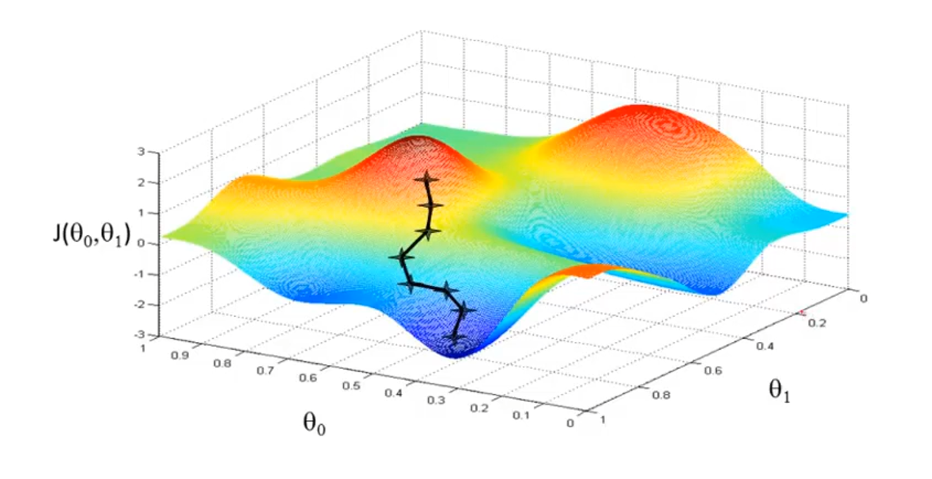
梯度下降(gradient descent)
似乎只找到局部最优解
a:=b 赋值
a = b 真假判断

converge(收敛) diverge(发散)
线性回归的代价函数总是convex function(凸函数) bow - shape
“Batch”:Each step of gradient descent uses all the training examples
多变量线性回归

其中X_0 为 1,这是为了适应计算机索引(从0开始)并不破坏原有顺序而添加的。
代价函数J对θ求偏导,其中x,y均为常量,h(x)是与θ有关的线性函数

多元梯度下降
特征缩放
是为了加快梯度下降速度,减少收敛所需次数。
不需要特别精确,只需使得特征在一相似范围内,一般约束到[-1,1]左右(接近),区间范围不宜过大或过小
Xi := Xi/range
均值归一化
使得特征值具有为0的平均值,计算公式如下:

调试
debug : making sure gradient descent is working correctly.
(a)画出J(θ)与迭代次数的关系曲线图,直观得出结果
(b)自动判断if J(θ) < ε 则收敛
若 J(θ)随迭代次数而上升,则降低学习率α,但α太小,则梯度下降缓慢。
每3(10)倍取一个α值,选择合适的learning rate —- α
特征与多项式回归
特征的选择是自由的~ 取决于从什么角度来看问题,最终更拟合数据,建立更好的模型。
直线可能不太合适时,考虑多项式(注意特征缩放)。
正规方程
直接求解θ,与梯度下降不同。不需要特征缩放
(a)令偏导数为0,求解θ1、2、3…的值,计算可能复杂
(b)看成向量,公式求解
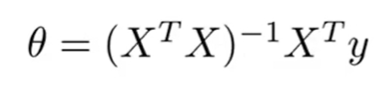
对于特征量小于10000的线性回归模型,正规方程比梯度下降优
正规方程在矩阵不可逆的情况下的solution
矩阵不可逆???
Octave中 ocpinv() inv()
两种方式优缺点对比
