机器学习-异常检测以及高斯分布

异常检测

给定样本，判断待测数据是否异常。

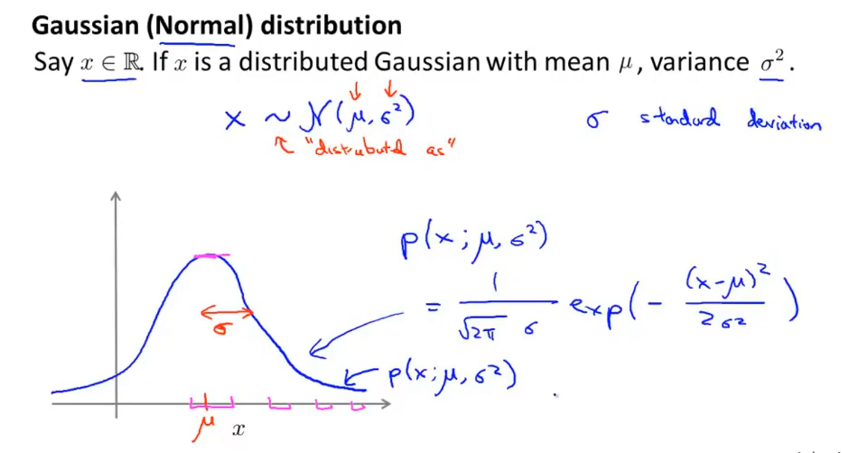
高斯分布

也称 正态分布，面积积分=1

高斯分布的参数极大似然估计

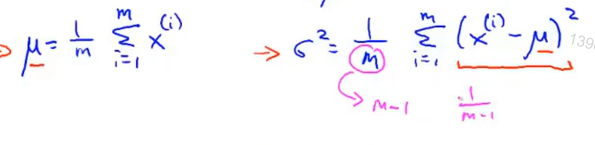
训练集中各特征量可以不是相互独立的

Π：对一系列数的乘积

算法流程

P(x)是对特征的建模

评估异常检测系统

用60%带标签的数据计算p(x),20%交叉验证集 20%测试集输出结果

然后计算准确率与召回率 ，F1从而评估异常检测系统

有点类似监督学习

异常检测 vs 监督学习

1 是异常的 0 是正常的

可能之后的特征跟现在不一致

使用

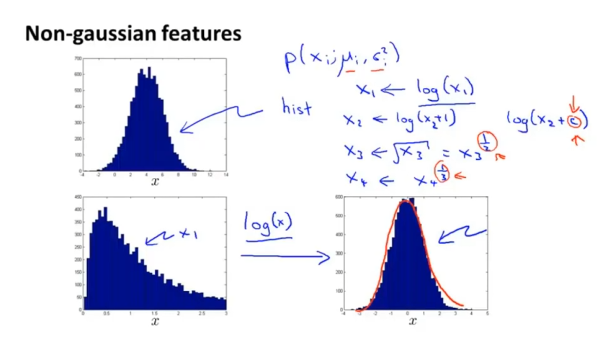
（1）转换非高斯分布特征

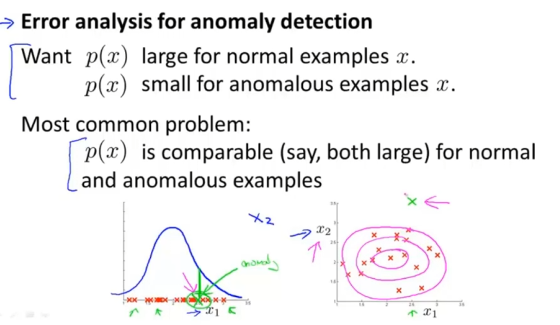
（2）误差分析，或添加新特征

多高斯分布

Σ 协方差矩阵 可体现特征间的相关性

μ 均值 集中点（概率较大的位置）

运用

单高斯与多高斯之间的联系

多高斯分布能够自然地捕捉特征之间的关系

而单高斯分布计算量小，适应大规模计算

所以在m>n时用多高斯分布

tips: Σ 如果是奇异矩阵即不可逆，可能有两种情况：

​ （1）没有满足m>n的条件

​ （2）存在冗余特征（高度线性相关的特征、不包含额外信息）

编程作业

estimateGaussian.m

function [mu sigma2] = estimateGaussian(X)
%ESTIMATEGAUSSIAN This function estimates the parameters of a 
%Gaussian distribution using the data in X
%   [mu sigma2] = estimateGaussian(X), 
%   The input X is the dataset with each n-dimensional data point in one row
%   The output is an n-dimensional vector mu, the mean of the data set
%   and the variances sigma^2, an n x 1 vector
% 

% Useful variables
[m, n] = size(X);

% You should return these values correctly
mu = zeros(n, 1);
sigma2 = zeros(n, 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the mean of the data and the variances
%               In particular, mu(i) should contain the mean of
%               the data for the i-th feature and sigma2(i)
%               should contain variance of the i-th feature.
%


mu = sum(X) / m;
sigma2 = sum((X-mu).^2) / m;

% =============================================================


end

selectThreshold.m

function [bestEpsilon bestF1] = selectThreshold(yval, pval)
%SELECTTHRESHOLD Find the best threshold (epsilon) to use for selecting
%outliers
%   [bestEpsilon bestF1] = SELECTTHRESHOLD(yval, pval) finds the best
%   threshold to use for selecting outliers based on the results from a
%   validation set (pval) and the ground truth (yval).
%

bestEpsilon = 0;
bestF1 = 0;
F1 = 0;

stepsize = (max(pval) - min(pval)) / 1000;
for epsilon = min(pval):stepsize:max(pval)
    
    % ====================== YOUR CODE HERE ======================
    % Instructions: Compute the F1 score of choosing epsilon as the
    %               threshold and place the value in F1. The code at the
    %               end of the loop will compare the F1 score for this
    %               choice of epsilon and set it to be the best epsilon if
    %               it is better than the current choice of epsilon.
    %               
    % Note: You can use predictions = (pval < epsilon) to get a binary vector
    %       of 0's and 1's of the outlier predictions


      predictions = (pval < epsilon);
      tp = sum( (predictions == 1) & (yval == 1) );
      fp = sum( (predictions == 1) & (yval == 0) );
      fn = sum( (predictions == 0) & (yval == 1) );;
      prec = tp / (tp+fp); 
      rec = tp / (tp+fn);
      F1 = 2*prec*rec / (prec+rec);
 % =============================================================

    if F1 > bestF1
       bestF1 = F1;
       bestEpsilon = epsilon;
    end
end

end