机器学习-支持向量机

机器学习最具有理论计算的部分，有点难

the Support Vector Machine (SVM)

监督学习算法

也称大间距分类器，因其设置了一个安全区域

在某些情况下比逻辑回归更适合构造非线性复杂分类器

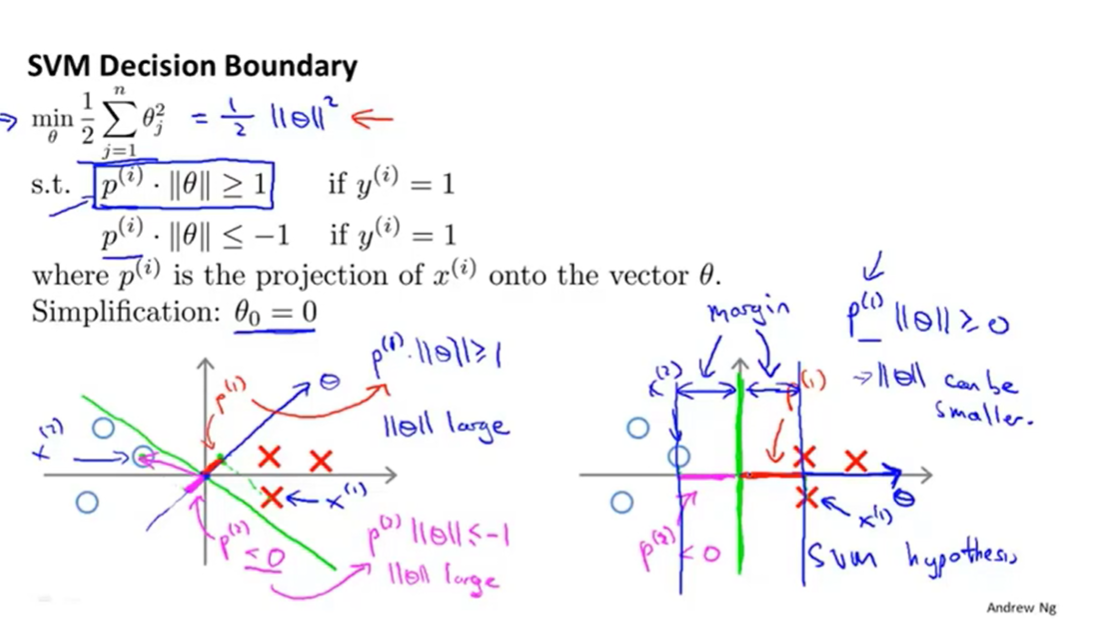
优化目标： 最小化假设函数，一样是找到最优的θ

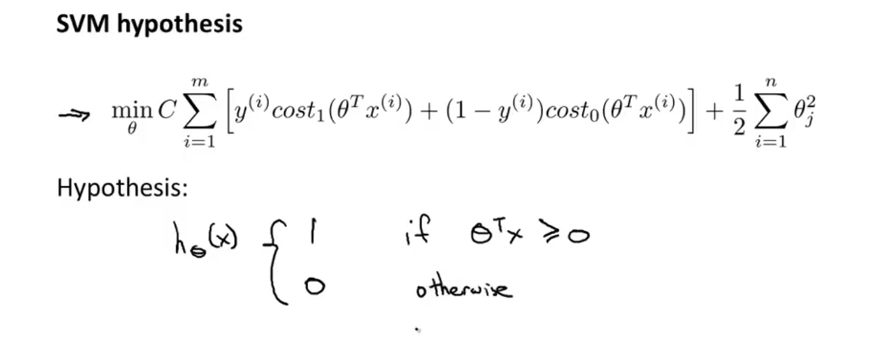
决策边界以最大的间距与训练集分开

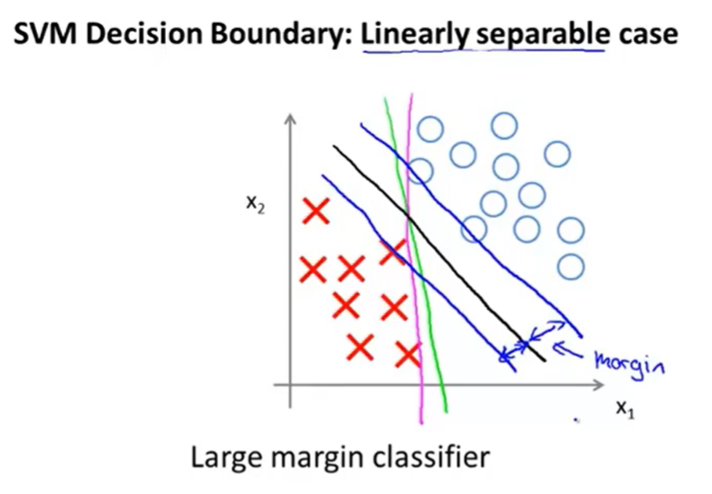
C过大 对异常点敏感 会导致训练集与边界线之间的间距变小。

向量内积的性质

其中 P 是 投影，有符号的实数

|| u|| 向量u的欧几里长度 就是 我们所说的“向量长度”

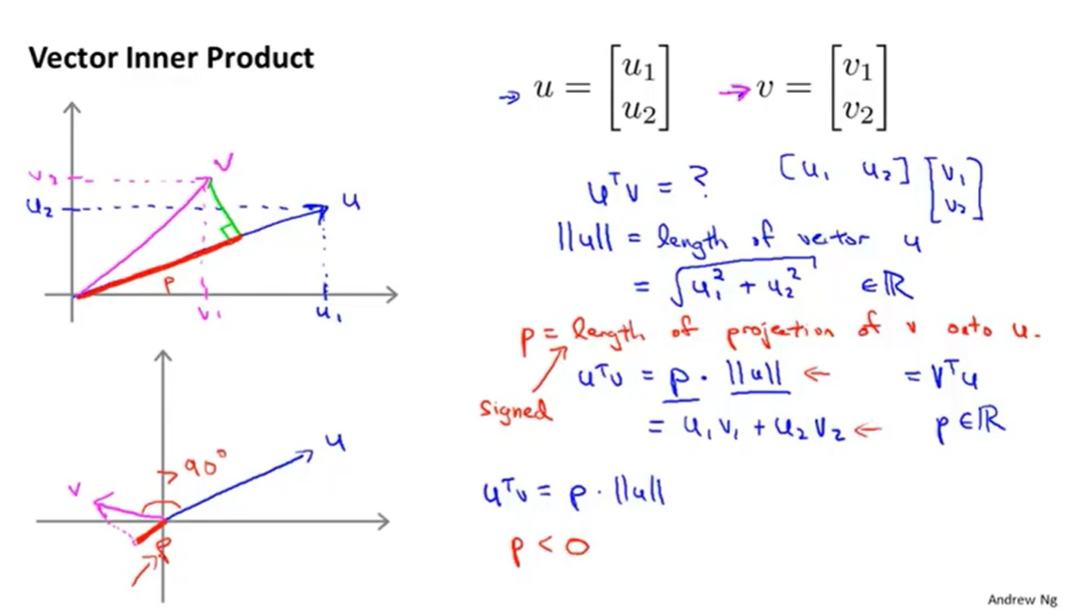
运用于代价函数的计算

θ的方向与决策边界90°正交

θ_0代表决策边界与Y轴的截距

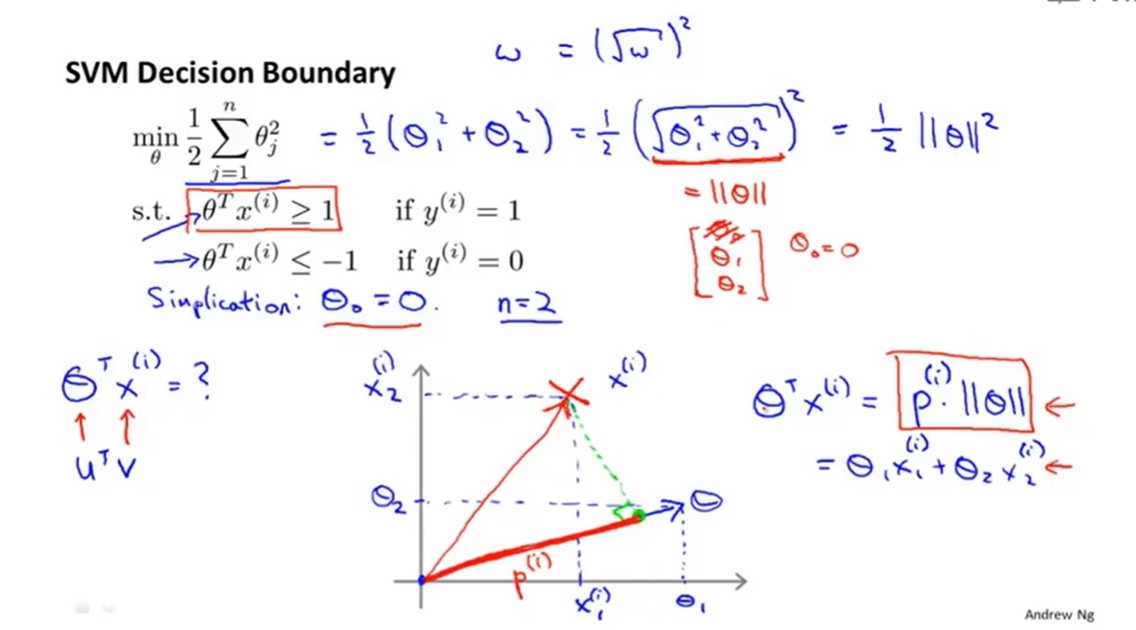
为什么支持向量机会找到最大间距呢？

如图它会使得P最大，从而min||θ||，P就是训练集在θ上面的投影，

在这样的过程中便找到了最大间距~

核函数

利用核函数K根据特征 X 和标记点 l 定义新的特征量 f

本质上 f是X与l的相似度

高斯核函数

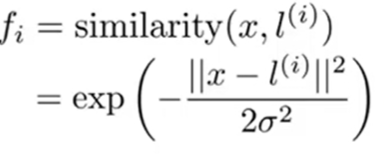
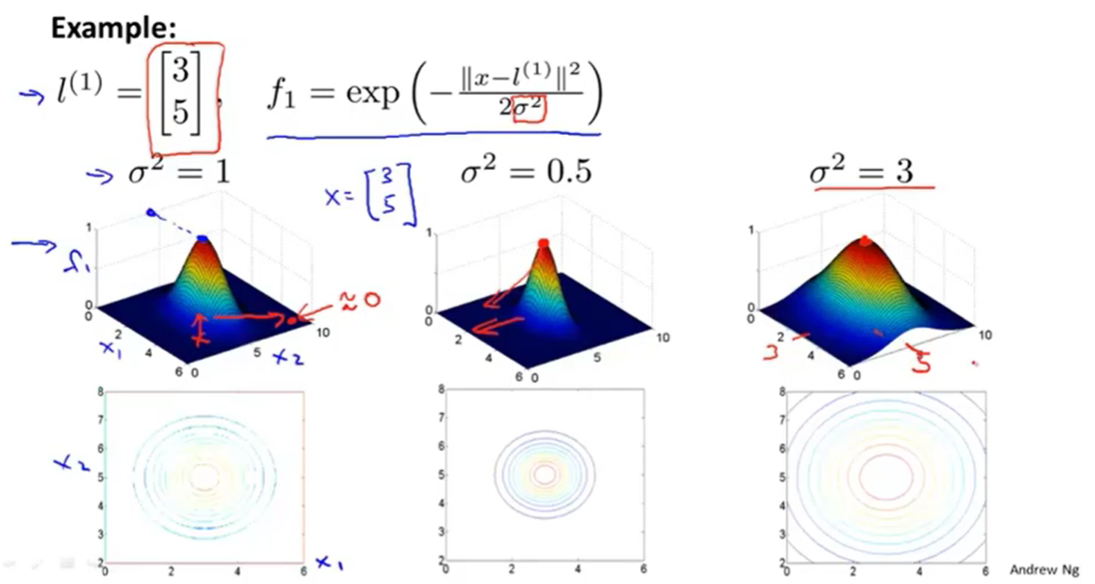
核函数与标记点共同定义复杂非线性决策边界

越大 特征量x从标记点l离开时变化速度越大

同样不需要正则化θ_0

θT M θ 更多的是为了计算效率，稍微改变了正则化的结果

参数的选择

C过大 相当于逻辑回归中 λ过小，不正则化 ，易出现过拟合；反之易出现欠拟合。

σ^2 过大 f变化过于平滑，易出现欠拟合；反之f变化剧烈易出现过拟合。

实现步骤

n表示特征量的数量，m表示训练集的数量

可以在n X多 ，m少的情况 不要核函数，得到一条线性决策边界

可以在m X多 ，n少的情况 选择高斯核函数，得到一条复杂非线性决策边界

在进行高斯核函数前不用特征归一化

多类别分类

类似于 逻辑回归中的“一对多” ，选择概率最大的 z

tips:

逻辑回归与不带核函数的支持向量机十分类似，效果略有不同。

神经网络适合大部分问题，但速度可能被限制

编程作业

gaussianKernel.m

function sim = gaussianKernel(x1, x2, sigma)
%RBFKERNEL returns a radial basis function kernel between x1 and x2
%   sim = gaussianKernel(x1, x2) returns a gaussian kernel between x1 and x2
%   and returns the value in sim

% Ensure that x1 and x2 are column vectors
x1 = x1(:); x2 = x2(:);

% You need to return the following variables correctly.
sim = 0;

% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return the similarity between x1
%               and x2 computed using a Gaussian kernel with bandwidth
%               sigma
%
%

sim = exp(- sum((x1-x2).^2)/2/(sigma^2));

% =============================================================
    
end

dataset3Params.m

function [C, sigma] = dataset3Params(X, y, Xval, yval)
%DATASET3PARAMS returns your choice of C and sigma for Part 3 of the exercise
%where you select the optimal (C, sigma) learning parameters to use for SVM
%with RBF kernel
%   [C, sigma] = DATASET3PARAMS(X, y, Xval, yval) returns your choice of C and 
%   sigma. You should complete this function to return the optimal C and 
%   sigma based on a cross-validation set.
%

% You need to return the following variables correctly.
C = 1;
sigma = 0.3;

% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return the optimal C and sigma
%               learning parameters found using the cross validation set.
%               You can use svmPredict to predict the labels on the cross
%               validation set. For example, 
%                   predictions = svmPredict(model, Xval);
%               will return the predictions on the cross validation set.
%
%  Note: You can compute the prediction error using 
%        mean(double(predictions ~= yval))
%
C_multi = [0.01,0.03,0.1,0.3,1,3,10,30];
sigma_multi = [0.01,0.03,0.1,0.3,1,3,10,30];
min_err =  Inf;

for i = 1:length(C_multi)
 for j = 1:length(sigma_multi) 
  model= svmTrain(X, y, C_multi(i), @(x1, x2) gaussianKernel(x1, x2, sigma_multi(j))); 
  predictions = svmPredict(model, Xval);
  err = mean(double(predictions ~= yval)); 
  if min_err > err
     C = C_multi(i);
     sigma = sigma_multi(j);
     min_err = err;
   endif
  endfor
endfor

% =========================================================================

end

processEmail.m

function word_indices = processEmail(email_contents)
%PROCESSEMAIL preprocesses a the body of an email and
%returns a list of word_indices 
%   word_indices = PROCESSEMAIL(email_contents) preprocesses 
%   the body of an email and returns a list of indices of the 
%   words contained in the email. 
%

% Load Vocabulary
vocabList = getVocabList();

% Init return value
word_indices = [];

% ========================== Preprocess Email ===========================

% Find the Headers ( \n\n and remove )
% Uncomment the following lines if you are working with raw emails with the
% full headers

% hdrstart = strfind(email_contents, ([char(10) char(10)]));
% email_contents = email_contents(hdrstart(1):end);

% Lower case
email_contents = lower(email_contents);

% Strip all HTML
% Looks for any expression that starts with < and ends with > and replace
% and does not have any < or > in the tag it with a space
email_contents = regexprep(email_contents, '<[^<>]+>', ' ');

% Handle Numbers
% Look for one or more characters between 0-9
email_contents = regexprep(email_contents, '[0-9]+', 'number');

% Handle URLS
% Look for strings starting with http:// or https://
email_contents = regexprep(email_contents, ...
                           '(http|https)://[^\s]*', 'httpaddr');

% Handle Email Addresses
% Look for strings with @ in the middle
email_contents = regexprep(email_contents, '[^\s]+@[^\s]+', 'emailaddr');

% Handle $ sign
email_contents = regexprep(email_contents, '[$]+', 'dollar');


% ========================== Tokenize Email ===========================

% Output the email to screen as well
fprintf('\n==== Processed Email ====\n\n');

% Process file
l = 0;

while ~isempty(email_contents)

    % Tokenize and also get rid of any punctuation
    [str, email_contents] = ...
       strtok(email_contents, ...
              [' @$/#.-:&*+=[]?!(){},''">_<;%' char(10) char(13)]);
   
    % Remove any non alphanumeric characters
    str = regexprep(str, '[^a-zA-Z0-9]', '');

    % Stem the word 
    % (the porterStemmer sometimes has issues, so we use a try catch block)
    try str = porterStemmer(strtrim(str)); 
    catch str = ''; continue;
    end;

    % Skip the word if it is too short
    if length(str) < 1
       continue;
    end

    % Look up the word in the dictionary and add to word_indices if
    % found
    % ====================== YOUR CODE HERE ======================
    % Instructions: Fill in this function to add the index of str to
    %               word_indices if it is in the vocabulary. At this point
    %               of the code, you have a stemmed word from the email in
    %               the variable str. You should look up str in the
    %               vocabulary list (vocabList). If a match exists, you
    %               should add the index of the word to the word_indices
    %               vector. Concretely, if str = 'action', then you should
    %               look up the vocabulary list to find where in vocabList
    %               'action' appears. For example, if vocabList{18} =
    %               'action', then, you should add 18 to the word_indices 
    %               vector (e.g., word_indices = [word_indices ; 18]; ).
    % 
    % Note: vocabList{idx} returns a the word with index idx in the
    %       vocabulary list.
    % 
    % Note: You can use strcmp(str1, str2) to compare two strings (str1 and
    %       str2). It will return 1 only if the two strings are equivalent.
    %

    for i = 1:length(vocabList)
        if strcmp(str,vocabList(i)) == 1
          word_indices = [word_indices ; i];
        endif     
    endfor

    % =============================================================


    % Print to screen, ensuring that the output lines are not too long
    if (l + length(str) + 1) > 78
        fprintf('\n');
        l = 0;
    end
    fprintf('%s ', str);
    l = l + length(str) + 1;

end

% Print footer
fprintf('\n\n=========================\n');

end

emailFeatures.m

function x = emailFeatures(word_indices)
%EMAILFEATURES takes in a word_indices vector and produces a feature vector
%from the word indices
%   x = EMAILFEATURES(word_indices) takes in a word_indices vector and 
%   produces a feature vector from the word indices. 

% Total number of words in the dictionary
n = 1899;

% You need to return the following variables correctly.
x = zeros(n, 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return a feature vector for the
%               given email (word_indices). To help make it easier to 
%               process the emails, we have have already pre-processed each
%               email and converted each word in the email into an index in
%               a fixed dictionary (of 1899 words). The variable
%               word_indices contains the list of indices of the words
%               which occur in one email.
% 
%               Concretely, if an email has the text:
%
%                  The quick brown fox jumped over the lazy dog.
%
%               Then, the word_indices vector for this text might look 
%               like:
%               
%                   60  100   33   44   10     53  60  58   5
%
%               where, we have mapped each word onto a number, for example:
%
%                   the   -- 60
%                   quick -- 100
%                   ...
%
%              (note: the above numbers are just an example and are not the
%               actual mappings).
%
%              Your task is take one such word_indices vector and construct
%              a binary feature vector that indicates whether a particular
%              word occurs in the email. That is, x(i) = 1 when word i
%              is present in the email. Concretely, if the word 'the' (say,
%              index 60) appears in the email, then x(60) = 1. The feature
%              vector should look like:
%
%              x = [ 0 0 0 0 1 0 0 0 ... 0 0 0 0 1 ... 0 0 0 1 0 ..];
%
%
for i=1:length(word_indices)
  
    x(word_indices(i)) = 1;
 
endfor

% =========================================================================
    

end