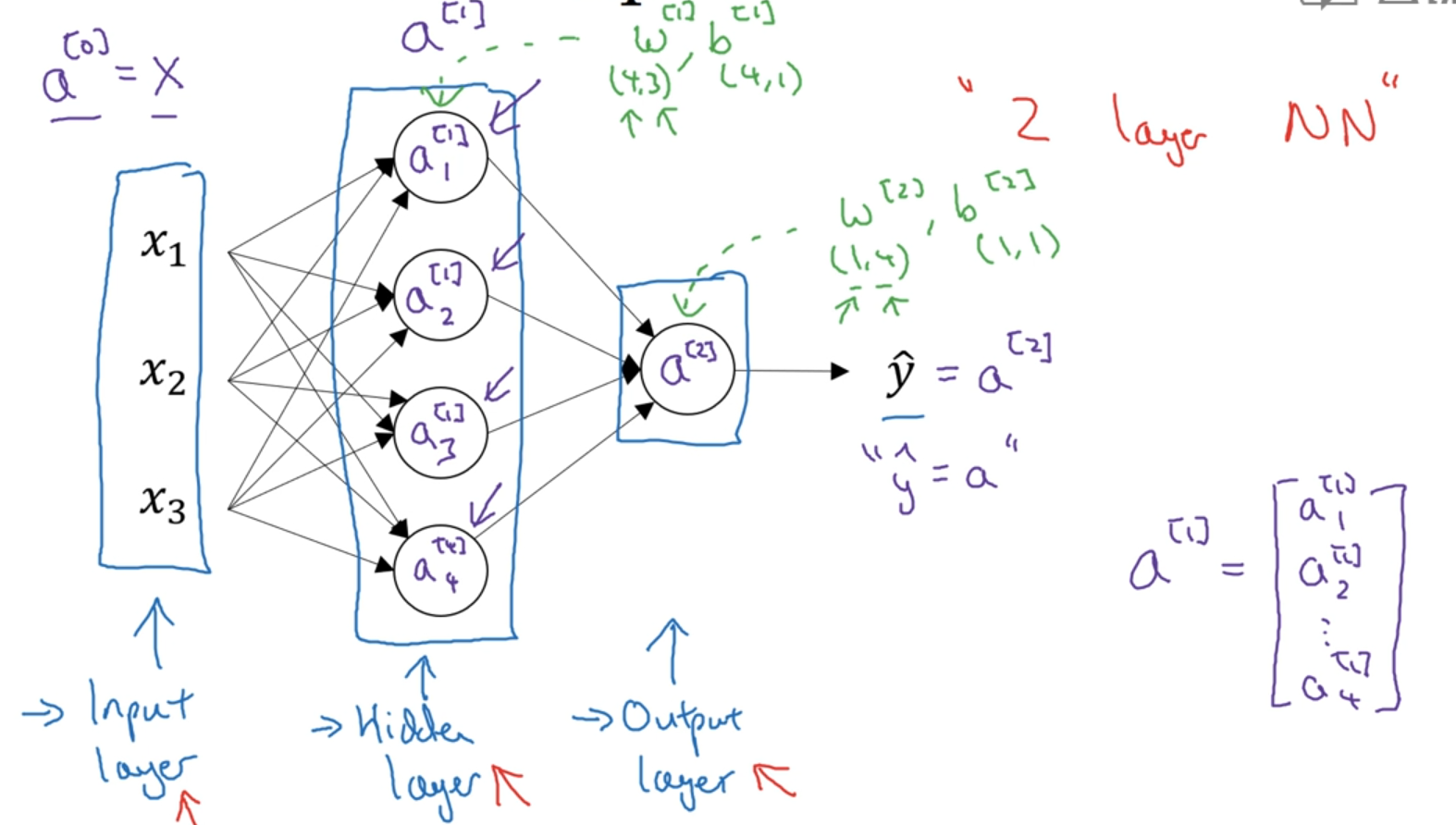
神经网络表示
a:activation —— 代表着网络中不同层传给下一层的值
a^(i)_j 第 i 层的第 j 的节点。
计算层数时不计入“输入层”,从隐藏层开始数
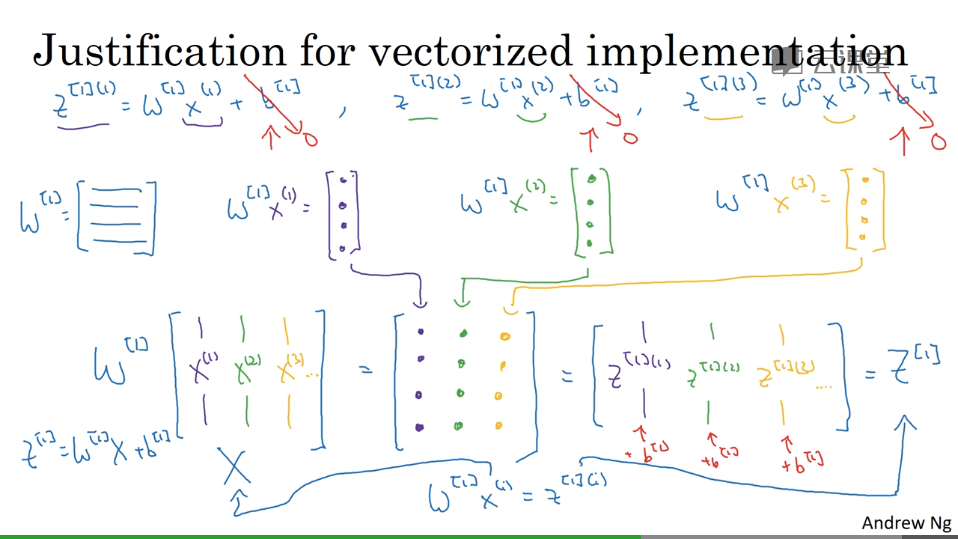
以逻辑回归为例

计算过程解释
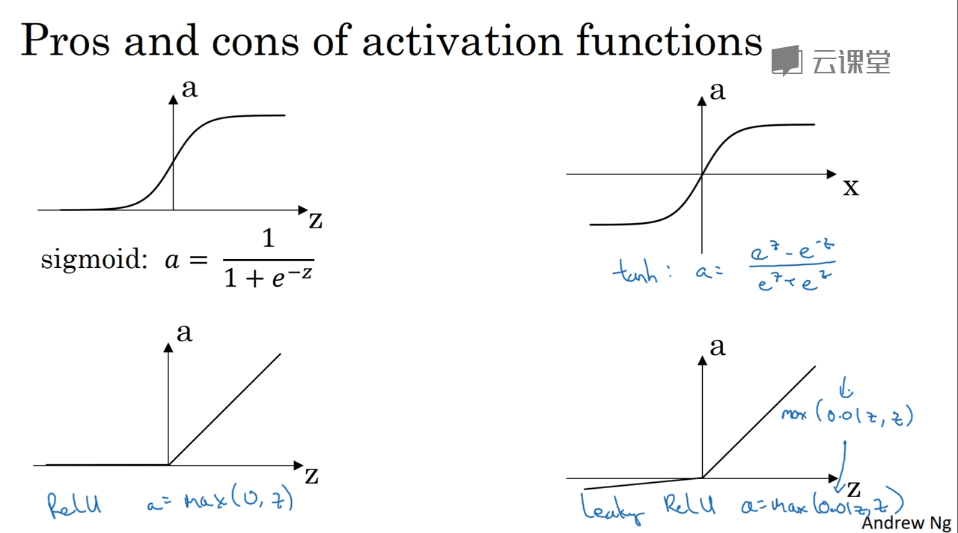
激活函数
种类
σ激活函数:除非用在二元分类的输出层,不然绝对不要用
tanh函数 在任何场合都具有优越性
ReLU函数 最常用的默认的激活函数 或者带泄露的ReLU函数
非线性激活函数
为了计算出更复杂的函数,必须引入非线性激活函数
只用线性激活函数的情况 (1)machine learning on regression problem(回归问题)
(2)输出层
(3)在隐藏层使用是与压缩有关的一些非常特殊的情况
导数
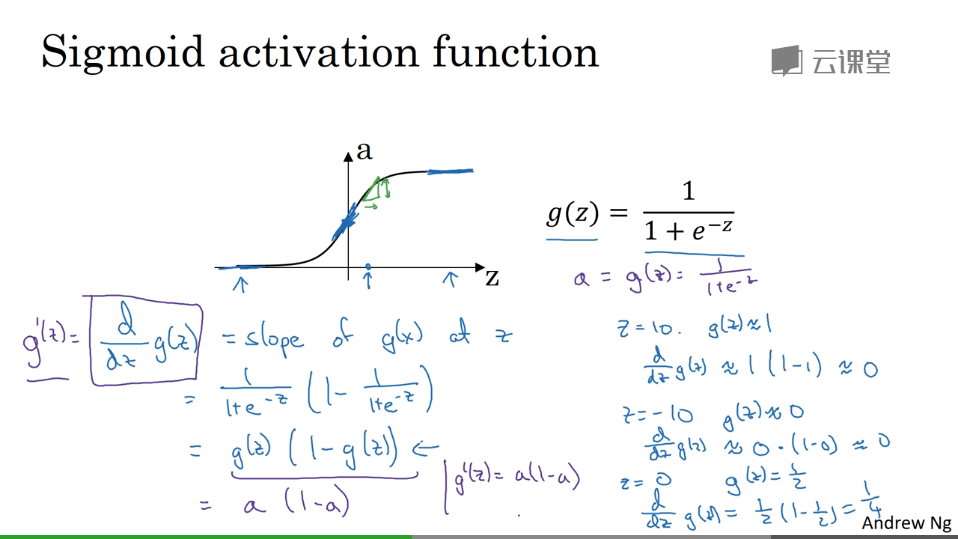
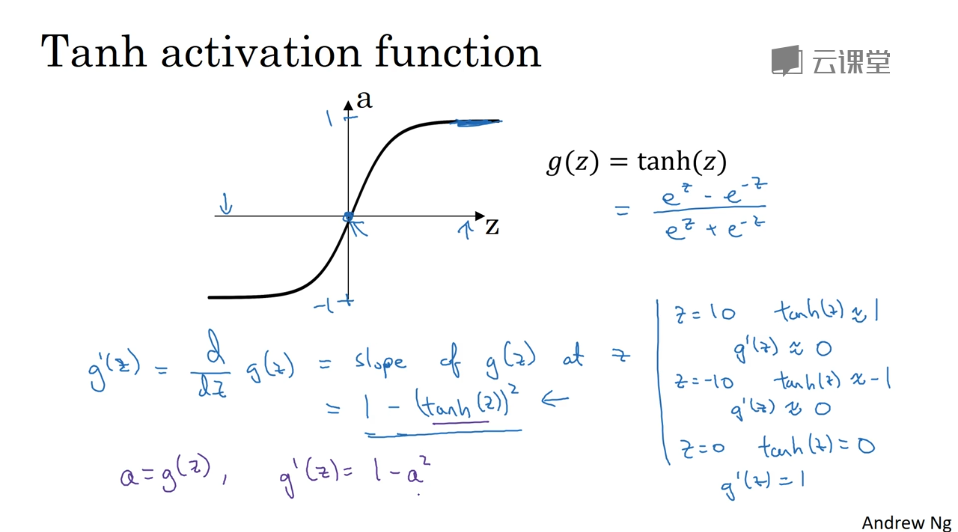

梯度下降
前向与反向传播(用到导数)
keepdims = true ,是为了防止python出现秩为1的矩阵(n, )
还有种方式是 不使用keepdims参数,而是显式调用reshape,将np.sum的结果写成矩阵形式

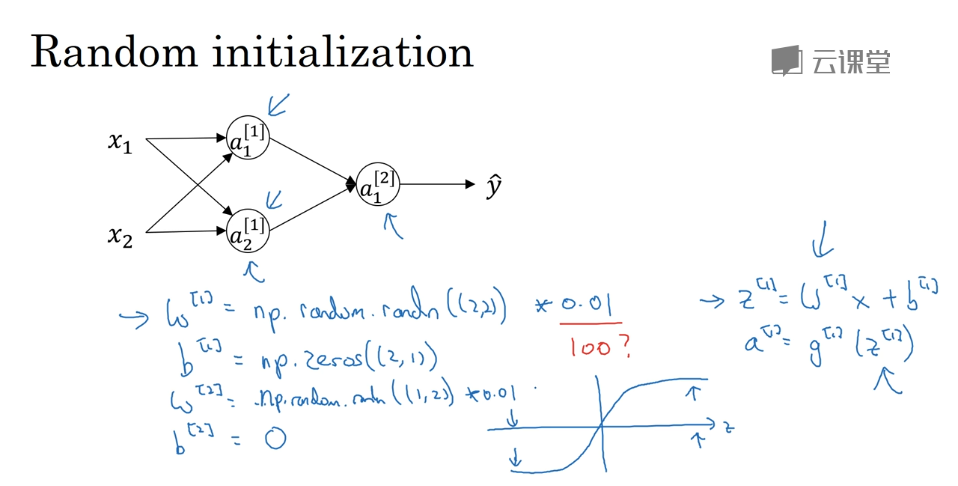
随机初始化
对于逻辑回归,可以将权重初始化为0
对于神经网络,各参数数组全部初始化为0 ,再使用梯度下降 将无效
因为隐藏层会计算完全一样的函数,出现对称性,权重一致无意义。
而我们需要不同的隐藏单元去计算不同的函数
解决方案:
随机初始化所有参数( 很小的值 )
示例: