机器学习-神经网络（前向传播）

原因

适应于非线性假设

sigmoid（logistic）activation function : 激活函数 指代 g(z)

X_0 偏置单元，值永远是1

θ 代表 参数或权重

架构

输入层-》隐藏层（不止一个）-》输出层

符号：

a(i)_j表示 第i层，第j个神经元或单元的激活项(由具体的神经元计算并输出的值)

θ(i) 表示 从第i层到第i+1层之间映射的权重矩阵

偏置单元省略没有写。

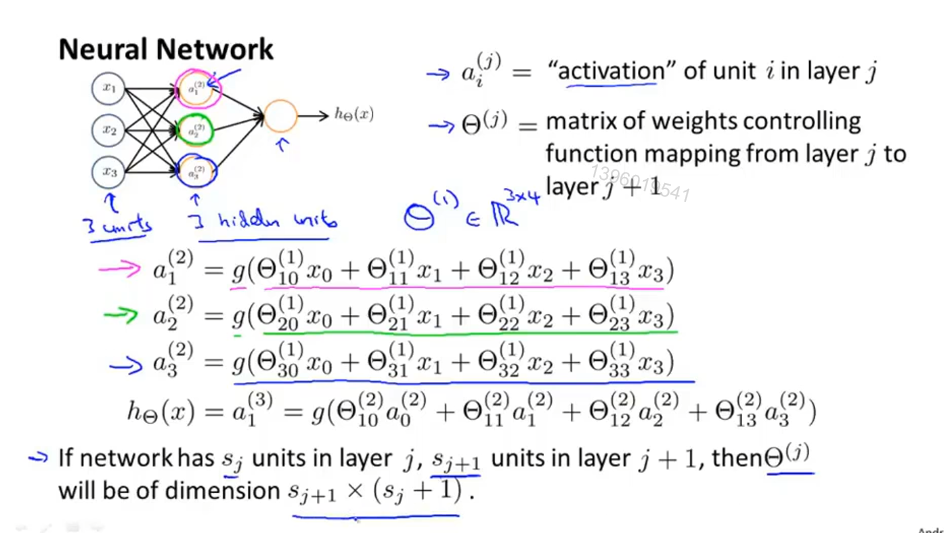
如果第 j 层中有 S_j 个单元，第 j+1 层中有 S_j+1 个单元，则θ(j)的维数： S_j+1*（ S_j + 1）

前向传播（向量化）

依次计算激活项，从输入项到输出项的过程。

下面是它的向量化实现

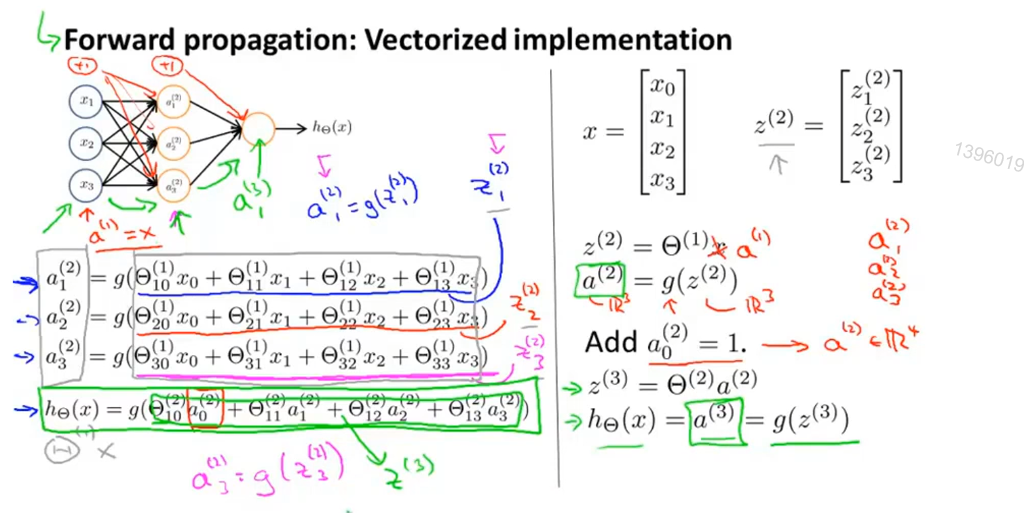
最后一层隐藏层到输出层 类似于 逻辑回归

多类别分类（一对多分类的扩展）

编程作业

displayData.m

function [h, display_array] = displayData(X, example_width)
%DISPLAYDATA Display 2D data in a nice grid
%   [h, display_array] = DISPLAYDATA(X, example_width) displays 2D data
%   stored in X in a nice grid. It returns the figure handle h and the 
%   displayed array if requested.

% Set example_width automatically if not passed in
if ~exist('example_width', 'var') || isempty(example_width) 
	example_width = round(sqrt(size(X, 2)));
end

% Gray Image
colormap(gray);

% Compute rows, cols
[m n] = size(X);
example_height = (n / example_width);

% Compute number of items to display
display_rows = floor(sqrt(m));
display_cols = ceil(m / display_rows);

% Between images padding
pad = 1;

% Setup blank display
display_array = - ones(pad + display_rows * (example_height + pad), ...
                       pad + display_cols * (example_width + pad));

% Copy each example into a patch on the display array
curr_ex = 1;
for j = 1:display_rows
	for i = 1:display_cols
		if curr_ex > m, 
			break; 
		end
		% Copy the patch
		
		% Get the max value of the patch
		max_val = max(abs(X(curr_ex, :)));
		display_array(pad + (j - 1) * (example_height + pad) + (1:example_height), ...
		              pad + (i - 1) * (example_width + pad) + (1:example_width)) = ...
						reshape(X(curr_ex, :), example_height, example_width) / max_val;
		curr_ex = curr_ex + 1;
	end
	if curr_ex > m, 
		break; 
	end
end

% Display Image
h = imagesc(display_array, [-1 1]);

% Do not show axis
axis image off

drawnow;

end

lrCostFunction.m

function [J, grad] = lrCostFunction(theta, X, y, lambda)
%LRCOSTFUNCTION Compute cost and gradient for logistic regression with 
%regularization
%   J = LRCOSTFUNCTION(theta, X, y, lambda) computes the cost of using
%   theta as the parameter for regularized logistic regression and the
%   gradient of the cost w.r.t. to the parameters. 

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;
grad = zeros(size(theta));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
%               You should set J to the cost.
%               Compute the partial derivatives and set grad to the partial
%               derivatives of the cost w.r.t. each parameter in theta
%
% Hint: The computation of the cost function and gradients can be
%       efficiently vectorized. For example, consider the computation
%
%           sigmoid(X * theta)
%
%       Each row of the resulting matrix will contain the value of the
%       prediction for that example. You can make use of this to vectorize
%       the cost function and gradient computations. 
%
% Hint: When computing the gradient of the regularized cost function, 
%       there're many possible vectorized solutions, but one solution
%       looks like:
%           grad = (unregularized gradient for logistic regression)
%           temp = theta; 
%           temp(1) = 0;   % because we don't add anything for j = 0  
%           grad = grad + YOUR_CODE_HERE (using the temp variable)
%

h = sigmoid(X * theta);
J =  sum((y-1)' *log(1-h) - y' *log(h))/m + lambda/2/m * (sum(theta.^2) - theta(1)^2);
grad = (X'*(h-y) + theta*lambda) / m;
grad(1) = grad(1) - lambda/m*theta(1);





% =============================================================

grad = grad(:);

end

oneVsAll.m

function [all_theta] = oneVsAll(X, y, num_labels, lambda)
%ONEVSALL trains multiple logistic regression classifiers and returns all
%the classifiers in a matrix all_theta, where the i-th row of all_theta 
%corresponds to the classifier for label i
%   [all_theta] = ONEVSALL(X, y, num_labels, lambda) trains num_labels
%   logistic regression classifiers and returns each of these classifiers
%   in a matrix all_theta, where the i-th row of all_theta corresponds 
%   to the classifier for label i

% Some useful variables
m = size(X, 1);
n = size(X, 2);

% You need to return the following variables correctly 
all_theta = zeros(num_labels, n + 1);

% Add ones to the X data matrix
X = [ones(m, 1) X];

% ====================== YOUR CODE HERE ======================
% Instructions: You should complete the following code to train num_labels
%               logistic regression classifiers with regularization
%               parameter lambda. 
%
% Hint: theta(:) will return a column vector.
%
% Hint: You can use y == c to obtain a vector of 1's and 0's that tell you
%       whether the ground truth is true/false for this class.
%
% Note: For this assignment, we recommend using fmincg to optimize the cost
%       function. It is okay to use a for-loop (for c = 1:num_labels) to
%       loop over the different classes.
%
%       fmincg works similarly to fminunc, but is more efficient when we
%       are dealing with large number of parameters.
%
% Example Code for fmincg:
%
%     % Set Initial theta
%     initial_theta = zeros(n + 1, 1);
%     
%     % Set options for fminunc
%     options = optimset('GradObj', 'on', 'MaxIter', 50);
% 
%     % Run fmincg to obtain the optimal theta
%     % This function will return theta and the cost 
%     [theta] = ...
%         fmincg (@(t)(lrCostFunction(t, X, (y == c), lambda)), ...
%                 initial_theta, options);
%

for c = 1:num_labels
  
  initial_theta = zeros(n+1 , 1);
  options = optimset('GradObj', 'on', 'MaxIter', 50);
  initial_theta = fmincg(@(t)(lrCostFunction(t, X, (y==c), lambda)),initial_theta,options);
  all_theta(c,:) = initial_theta';

end

% =========================================================================


end

predict.m

function p = predict(Theta1, Theta2, X)
%PREDICT Predict the label of an input given a trained neural network
%   p = PREDICT(Theta1, Theta2, X) outputs the predicted label of X given the
%   trained weights of a neural network (Theta1, Theta2)

% Useful values
m = size(X, 1);
num_labels = size(Theta2, 1);

% You need to return the following variables correctly 
p = zeros(size(X, 1), 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
%               your learned neural network. You should set p to a 
%               vector containing labels between 1 to num_labels.
%
% Hint: The max function might come in useful. In particular, the max
%       function can also return the index of the max element, for more
%       information see 'help max'. If your examples are in rows, then, you
%       can use max(A, [], 2) to obtain the max for each row.
%

one = ones(size(X,1),1);

addX = [one,X];
z = addX * Theta1';
a = sigmoid(z);
addA = [one,a];
h = addA * Theta2';

maxRow = zeros(size(X,1) ,1);
for i =1:m
  [maxRow(i), p(i)] = max(h(i,:));
endfor


% =========================================================================


end

predictOneVsAll.m

function p = predictOneVsAll(all_theta, X)
%PREDICT Predict the label for a trained one-vs-all classifier. The labels 
%are in the range 1..K, where K = size(all_theta, 1). 
%  p = PREDICTONEVSALL(all_theta, X) will return a vector of predictions
%  for each example in the matrix X. Note that X contains the examples in
%  rows. all_theta is a matrix where the i-th row is a trained logistic
%  regression theta vector for the i-th class. You should set p to a vector
%  of values from 1..K (e.g., p = [1; 3; 1; 2] predicts classes 1, 3, 1, 2
%  for 4 examples) 

m = size(X, 1);
num_labels = size(all_theta, 1);

% You need to return the following variables correctly 
p = zeros(size(X, 1), 1);

% Add ones to the X data matrix
X = [ones(m, 1) X];

% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
%               your learned logistic regression parameters (one-vs-all).
%               You should set p to a vector of predictions (from 1 to
%               num_labels).
%
% Hint: This code can be done all vectorized using the max function.
%       In particular, the max function can also return the index of the 
%       max element, for more information see 'help max'. If your examples 
%       are in rows, then, you can use max(A, [], 2) to obtain the max 
%       for each row.
%  

% size(h) = 50000*10   h保存的是预测5000个数据所属label的概率情况  
h = sigmoid(X * all_theta');

rowMax = zeros(size(X,1),1);
%这是取每行(最后一个参数：2)最大值 ps:取每列(最后一个参数：1)最大值
%rowMax = max(h,[],2);

%取每行最大值的索引值
for i = 1:m
 [rowMax(i), p(i)] = max(h(i,:));
end

% =========================================================================

sigmoid.m

function g = sigmoid(z)
%SIGMOID Compute sigmoid functoon
%   J = SIGMOID(z) computes the sigmoid of z.

g = 1.0 ./ (1.0 + exp(-z));
end