TSM2: Optimizing Tall-and-Skinny Matrix-Matrix Multiplication on GPUs
Publication: ICS ‘19: Proceedings of the ACM International Conference on SupercomputingJune 2019 Pages 106–116
论文链接：https://doi.org/10.1145/3330345.3330355
源码链接：https://GitHub.com/codyjrivera/tsm2-imp
摘要
线性代数运算已广泛用于大数据分析和科学计算中。在优化具有规则形状输入的GPU上的线性代数运算方面，已经完成了许多工作。但是，当输入不是常规形状时，很少有工作专注于充分利用GPU资源。当前的优化缺乏考虑充分利用内存带宽和计算能力的优势，因此它们只能实现次优性能。在本文中，我们提出了一种在GPU上高效的高瘦矩阵乘法算法-TSM2。它着重于优化无规则输入的线性代数运算。我们实施提出的算法并在三种不同的Nvidia GPU微体系结构上进行测试：开普勒，麦克斯韦和帕斯卡尔。实验表明，我们的TSM2将计算速度提高了1.1到3倍，与当前的最新技术相比，内存带宽利用率提高了8％-47.6％，计算能力利用率提高了7％-37.3％。我们用TSM2取代了K均值和基于算法的容错（ABFT）中的原始矩阵运算，并实现了高达1.89倍和1.90倍的加速。
1 介绍
矩阵乘法((GEMM))是大数据分析和科学计算中应用最广泛的线性代数运算之一。由于多种因素(如算法、输入数据等)的影响，GEMM的输入矩阵在不同的应用中大小或形状往往是不同的。例如，许多现代的高度可伸缩的科学仿真包针对流体动力学的领域，如有限元法，需要用较小的输入矩阵来计算大量的GEMM。人工神经网络(ANN)涉及使用GEMM与中小输入矩阵。矩阵分解使用GEMM和大尺寸的输入矩阵[2,12,20,21]。因此，除了在过去几十年里已经被广泛优化的大规模输入外，中小型输入的GEMM也引起了最近研究人员的大量关注。例如，[14]提出了MAGMA-Batched，它的目标是将小的输入矩阵批处理成更大的矩阵，从而利用gpu上针对大输入大小的高度优化实现。[16]提出了利用现代CPU架构上的体系结构和指令级优化来加速小输入的GEMM。
虽然以往的研究主要集中在优化不同矩阵尺寸的GEMM，但大多数研究都假设输入矩阵是规则的。换句话说，他们在作品中提到的尺寸通常是指输入矩阵的两个维度。例如，一个小矩阵意味着它的宽度和高度都很小，它们的大小也很接近。然而，对于非规则形状的GEMM的优化工作做得并不多。例如，有一种特殊的不规则形状输入，其中两个维度的大小有显著的差异，即。,又高又瘦。据我们所知，对于带有粗细输入的GEMM还没有进行充分的研究和优化。粗细输入在许多应用程序中都有使用。例如，最近高度优化的K-means实现[1,13]使用GEMM作为其核心计算，由于中心体的数量通常远远小于输入数据点的数量，因此输入大小通常很小。也,当GEMM用于编码校验和许多ABFT应用程序(9ś11,17、18、22、28ś30),输入通常涉及一个又高又瘦的校验和权重矩阵。
以前为优化使用规则形状输入的GEMM所做的努力可能不适用于非规则形状输入。例如，[9]表明，使用供应商高度优化的线性代数库(例如cuBLAS[19])计算带有瘦长输入的GEMM比将瘦长输入矩阵分解成若干向量然后应用矩阵-向量乘法要慢。然而，可以很容易地看到，这种解决方案不是很有效，因为GPU访问输入矩阵中的元素的次数比需要的多。虽然可以通过将许多瘦而高的输入矩阵分组成类似于所提出的方法的大型输入矩阵来优化性能，但是在某些情况下这种分组方法是不可行的。例如，在用户流中，粗细输入矩阵可以一次一个地从生产者进程生成。将其中几个分组成一个大矩阵需要延长等待时间，这不适用于时间敏感的应用程序。另一方面，如果输入矩阵很大(例如，正形大矩阵与瘦长矩阵之间的乘法) ，内存空间可能会限制可以将其放入内存的总矩阵数。
在这项工作中，我们的目标是在GPU平台上使用瘦而高的输入来优化GEMM的计算，因为许多使用GEMM的应用程序都部署在GPU上。因此，我们的优化可以大大有利于这些应用。我们工作想法是：当输入矩阵大小regular-shaped(例如,一个nn矩阵乘以一个nn矩阵,输入矩阵中的每个元素加载到GPU需要O(n)计算),计算时间通常超过内存访问时间(特别是大型矩阵)。然后GEMM操作是计算限制的。然而,当输入矩阵的大小是高高瘦瘦的(nn矩阵乘以一个nk的矩阵，其中k远小于n, k矩阵的每个元素为只使用O(k)时间平均计算),根据k和执行之间的比率GPU峰值计算能力和内存峰值吞吐量,GEMM计算可以是计算(compute-bound)或内存(memory-bound)受限的。当k变小时，它受限于内存;否则，它将受限于计算。要使用瘦而高的输入来优化GEMM，设计同时考虑计算和内存受限情况的算法至关重要。
本文的主要贡献包括:
我们研究了当前最先进的GEMM实现的局限性。在基准测试中，我们发现GPU资源的利用率低是导致输入太窄或太大时性能低下的主要原因。
我们设计了一个基于GPU优化的针对于双精度和单精度瘦高输入的GEMM算法。我们将优化后的版本称为TSM2。利用输入大小和硬件结构特点的知识，我们重新设计了计算算法，以确保在有内存限制的情况下有高的内存带宽利用率，在有计算限制的情况下有高的计算性能。实验结果表明，与最先进的cuBLAS库相比，我们的TSM2可以获得1.1x-3倍的加速。我们还将K-means和ABFT应用中的原有GEMM操作替换为TSM2，并实现最高1.89x和1.90x的整体速度提升。
2 背景
2.1瘦高型矩阵输入的定义
在这项工作中，我们将范围限制为在gpu上瘦高输入的GEMM。瘦高输入尺寸意味着，对于两个输入矩阵，至少有一个矩阵是瘦高输入的(一个维度比另一个维度小得多)。例如，输入矩阵A的大小为2048020480和矩阵B的大小为204802在我们的工作中被认为是瘦高输入。在本文中，我们重点研究了具有一个规则的大输入矩阵和一个瘦高输入矩阵的GEMM的优化问题。本文将矩阵A称为较大的输入矩阵(nn)，将矩阵B (nk)称为瘦高型输入矩阵。我们选择这种输入的大小和形状，是因为我们相信它可以暴露各种瘦高输入的大部分挑战，所以本文介绍的设计思想和优化技术可以很容易地应用于其他稍有修改的情况。此外，我们选择让较大的矩阵是方形的，只是为了简化表示。我们的优化可以与其他非方形输入达到类似的效果。
2.2 cuBLAS
cuBLAS库为GPU优化的最常用的标准线性代数库之一是由Nvidia开发的。cuBLAS是许多大数据和科学计算应用的核心计算库。例如，它是MAGMA异质线性代数库[15,23,24]、cuLA库[6]、cuDNN深度学习库[5]的GPU计算库。通过Nvidia的深度优化，cuBLAS库能够在许多用例中提供最先进的性能。例如，使用大的规则形状的输入矩阵，他们的GEMM实现可以达到GPU[3]的接近峰值的性能。
然而，我们发现GEMM子程序在某些输入矩阵大小为[11]的情况下没有得到充分优化。例如，在瘦高输入情况下，当前最佳实现中的GEMM操作(运行在NVIDIA Tesla K40c GPU上的cuBLAS 9.0)在k = 2时平均只使用了理论峰值内存带宽的不到10%(图5 (a) - (b))。当k = 16时，相同的GEMM操作平均只使用理论峰值内存带宽的20%以下(图5 (g) - (h))。输入维度越大，资源利用率越低。通过比较两种输入的大小，可以看出，对于k值较小的输入，计算占用了较高的内存带宽(接近内存限制)。另一方面，对于k值较大的输入，计算会使用较高的计算能力(接近于计算限制)。但是，由于我们无法分析GEMM在非开源cuBLAS库中的实现，因此很难准确地描述它们的计算特性。
3 优化设计
3.1 对输入大小的洞察
对于规则型GEMM (nn矩阵乘以nn矩阵)，输入矩阵大小为O(n2)，计算时间复杂度为O(n3)，因此在整个计算过程中，输入矩阵中的每个元素都被使用O(n)次。由于加载数据从GPU的芯片DRAM(即。对于GPU来说，这类问题的一个常见的优化是通过使用快速的片上内存**(如缓存、寄存器)来实现数据重用，从而最小化每个元素加载到GPU的次数，从而避免了大量的数据加载操作。**随着负载数量的减少，优化的GEMM趋向于计算限制。例如，当前cuBLAS库中的GEMM实现在gpu[3]上可以达到近乎裸机的性能。然而，与常规形状的GEMM不同，当输入大小为瘦而高时，输入矩阵的大小仍然是O(n2)，但是计算时间复杂度是O(n2k)。因此，输入矩阵中的每个元素平均使用k次:
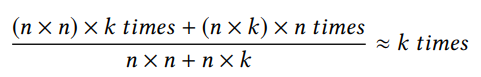
根据k的大小和目标GPU的峰值计算能力和内存吞吐率，TSM2可以是计算限制的，也可以是内存限制的。当k变小时，计算趋向于内存限制。否则，问题将趋向于计算限制。在这两种情况下，问题总是在内存限制和计算限制，因此设计针对这两种情况都进行优化的算法是至关重要的。
3.2 算法设计
算法设计作为优化的核心，起着非常重要的作用。首先，我们需要考虑如何将TSM2的工作负载转换为CUDA的编程模型(即,线程层次结构)。
虽然工作负载可以很容易地分解成许多独立的较小的工作负载，但是仍然需要仔细考虑工作负载的分布，因为任何不必要的性能损失都会严重地导致GPU资源的利用率不足。我们的设计考虑了以下几个因素:
(1)全局内存访问的总次数;
(2)全局内存吞吐量的效率;
(3)全局内存吞吐量利用率;
(4)总体工作量的并行性;
(5)片内存储器利用率;
(6)流式多处理器(SM)利用率;
(7)计算和内存绑定情况的优化。
为了获得良好的性能，在GPU的每个SM中必须存在足够数量的活动线程，以确保正确的指令和内存访问延迟隐藏。因此，在我们的算法中，我们通过将矩阵**A的n行分配给n个不同的线程来分配工作负载。每个向量矩阵乘法被分配给一个线程(即(A[i,:]*B))**。其优点有三:1)保证了高并行度和高SM占用率;2)由于矩阵A的元素个数远大于矩阵B，这种分布保证了有利于矩阵A的最小内存访问次数;3)它还支持高内存访问效率和吞吐量，因为所有对矩阵A的内存访问都是自然合并的(假设矩阵按惯例存储在column-major(列优先)中)。
对于分配给每个线程的向量-**矩阵乘法，为了进一步减少对矩阵A**的内存访问次数，我们使用矢量积计算代替常规的内积式计算。如Alg. 1所示，如果我们使用内积，矩阵A的每个元素被重复引用k次。另一方面，如果我们使用Alg. 2中所示的外积，则矩阵A的每个元素只被引用一次。(请注意，正如我们将在后面的部分中讨论的，当k大于某个阈值时，由于每个线程可用的资源有限，矩阵a中的元素仍然需要被引用多次，但它仍然比使用内积低得多)。对于大的矩阵A来说，这样做的好处是显著的，因为它大大减少了整个GEMM计算过程中全局内存访问的总数。而且，与内积相比，矢量积不会给矩阵B带来任何额外的内存访问。外部产品的唯一成本是持有k个中间结果的额外寄存器。但是，通过适当的调优，与额外的内存访问相比，它们只会带来很少的性能影响。
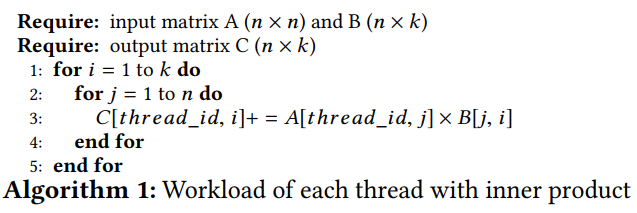
3.3 高效的芯片外内存访问
优化内存密集型应用的一个关键因素是确保高芯片内存访问效率。根据GPU模型类型或运行时配置,全局内存(ofchip)访问的线程在相同的变形可以合并到128字节或32字节处理[4]如果他们访问相同地址分为128字节或32字节段全局内存,则高效使用内存带宽。否则，GPU仍然在128字节或32字节的处理中加载内存。
但它可能包含存储在邻居地址中的未请求数据，这将导致频繁的内存访问。由于每个线程读取矩阵A的一行，并且按照惯例将矩阵存储在column-major中，因此，当相同warp访问元素中的线程位于不同行的不同列上时，内存访问自然会合并在一起。因此，在矩阵a上实现了100%的内存访问效率。而在矩阵B上，所有线程同时访问同一个元素，导致单个内存包含一个被请求的元素和多个未请求的邻居元素。因此，只有128/8字节= 6.25%或8字节/32字节= 25%的内存访问效率达到访问64位双精度浮点数。尽管矩阵B中元素的总数很少，但是考虑到每个元素需要被访问n次，这种不合理的访问模式仍然会极大地影响整体性能。为了提高对矩阵**B的访问效率，我们在GPU中使用了共享内存。**由于它位于芯片上，共享内存给我们的速度L1缓存，它是完全可编程的。一个线程块中的线程可以使用共享内存来共享数据。因此，共享内存的一个关键优势是它消除了数据加载模式和数据使用模式之间的一致性需求，这使我们能够以最有效的方式加载全局内存，并保持我们使用数据的方式与以前一样。
通过使用共享内存访问矩阵B，我们可以减少总的内存访问次数，并合并内存访问。如Alg. 3所示，对于每个迭代，我们现在让一个线程块协同工作，以一种合并兼容的方式(第13-15行)将一个矩阵B块获取到共享内存中，而不是让线程单独地请求它们需要的元素。然后在计算期间，每个线程通过共享内存引用矩阵B中的元素，而不是从全局内存中分别加载它们。这减少了从全局内存访问矩阵B的总次数(每个元素从n到n/t1)。此外，同一线程块中的线程(同warp)逐列获取矩阵B中的元素，从而能合并式内存访问。这大大提高了矩阵B的内存访问效率，达到100%。在Alg. 3中，我们还引入了三个参数:t1、t2和t3。这些参数用于调整性能，将在后面的部分中进行讨论。
3.4 优化共享内存的使用
虽然速度很快，但是在使用[7]之前，仍然需要将共享内存中的元素加载到寄存器中。它的访问速度直接影响到系统的整体性能。为了快速并行访问，共享内存被划分为几个相同大小的内存库。不同的线程可以同时访问不同的内存库。因此，与单个内存库的吞吐量相比，整个b内存banks可以将总体共享内存吞吐量提高至多b倍。但是，如果同一warp中的x个线程从同一存储库访问不同的数据，就会发生x-way bank冲突，每个请求都会发生x-way bank 冲突，这极大地降低1/x的访问吞吐量。
在我们的算法中，同一线程中的线程块将数据从全局内存一列一列地加载到共享内存中，以支持快速合并的全局内存访问。然后，线程在计算期间逐行访问共享内存中的数据。我们如何在共享内存中存储元素将影响到如何从内存bank访问这些元素，从而影响到共享内存的吞吐量。我们有两种方法在共享内存中存储矩阵**B:**列主存储和行主存储。要在这两种方式中做出选择，我们需要分析和比较哪一种方式带来的总体bank冲突最少。为了简单起见，我们假设矩阵B的每一块的大小是t1*t2, t1是banks b的总数量的乘积。
对于以列为主的存储，矩阵B的一个块的同一列中的元素(32位words或64位words)存储在连续的存储banks中。对共享内存与b banks,每一个t1的一列元素存储在连续b banks中，每个bank存储最多t1/b的元素和最多同时访问（warp size / b）个线程。如果（warp size / b）大于1，这可能导致bank冲突。
对于以行为主存储器，矩阵B的同一行中的元素存储在连续的存储banks中。因此，同一列的元素存储在（b/t2）个不同的 bank 中，每个bank存储来自同一列的（t1*t2/b）元素。由于每个bank的一列元素数是原来的t2倍，所以每个bank在同一时间访问的线程数最多是原来的t2倍: （warp size / b） t2，这也可能导致bank冲突.
在现代的Nvidia gpu上，warp size被fixed到32，banks的总数也是32[4]，所以列主存储器不会引起banks冲突，因为每个bank最多只能有一个线程访问。行主存储器会导致多达t2-way bank conlict，这会将总体共享内存吞吐量降低到峰值吞吐量的1/t2。如图1所示，我们使用列主存储器(左侧)和行主存储器(右侧)将一个64*2矩阵块加载到共享内存中。当使用列主存储器时，在同一warp上的线程访问不同的banks，因此不发生bank冲突。另一方面，当使用行主存储器时，32个元素被存储在16个bank中，导致2-way bank conflict.
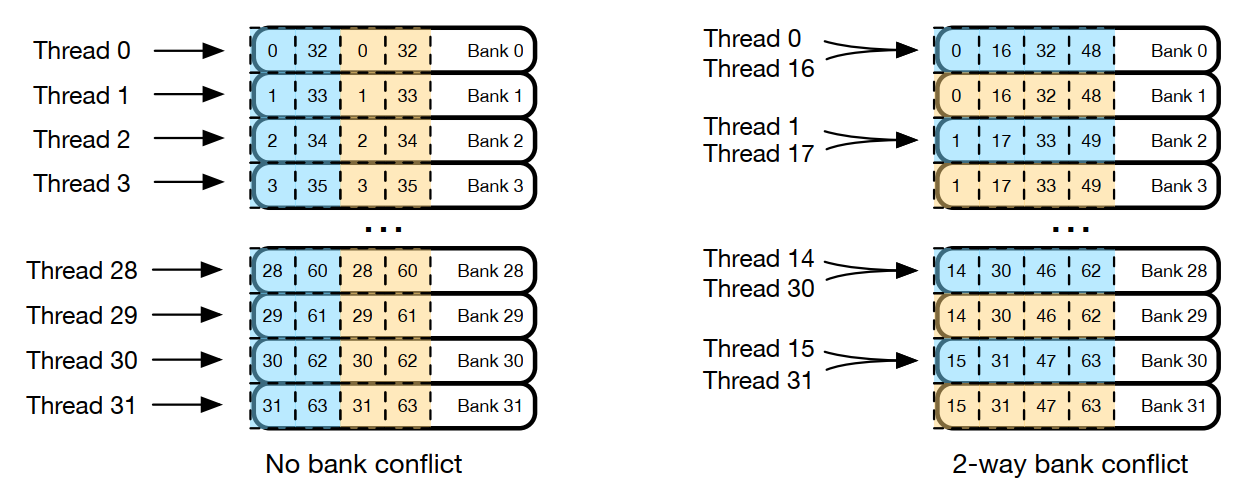
图1:在共享内存中存储64*2的矩阵B时，将列-主(左)和行-主(右)存储进行比较。蓝色和黄色的方块代表第一列和第二列中的元素。当32个线程访问一列中的32个元素时(例如，第一列的元素0到31)，主列存储不会带来bank冲突，而行主列存储产生2-way bank conflict.，这会减少一半的吞吐量。
在我们的算法，当访问共享内存中的元素进行计算时，一个warp的线程每次访问相同元素。虽然多个线程正在访问一个 bank ，但它们访问的是相同的元素，因此只启动一次广播，这不会导致 bank conflict。这对两种存储方式都是一样的。因此，我们选择列主存储，因为它不会带来bank conflict，并可能带来最高的共享内存吞吐量。
3.5 计算内存重叠与访问延迟
在执行过程中，对于每个指令的发出时刻，每个warp调度器都会选择一个合适的warp并将其发送到相应的组件中执行。只有当下一条指令的所有操作数都准备好时，warp才有资格使用。但是，如果warp从全局内存中加载数据，则需要几百个周期才能准备好执行。为了隐藏这种长时间的延迟，我们可以增加每个SM中线程的数量，以确保始终存在合适的warps[25]，或者在数据加载和数据使用操作之间放置独立的指令，以便warps也可以在内存加载期间执行。第一种方法要求我们调整每个线程块的片上资源使用。我们将在下一节中讨论。在本节中，我们的目标是在数据加载和数据使用操作之间添加独立的指令。
在Alg. 3中显示，第13-15和18-20行从全局内存加载数据，第21-23行在数据加载后使用数据。然而，由于数据依赖，中间没有独立的指令，所以一旦每个warp发出全局内存访问请求，它必须等待被请求的元素准备好，然后才能进行计算。
因此，为了添加独立的指令，我们使用数据预取来混合相邻迭代之间的数据加载和使用。具体来说，我们不让每个迭代加载将用于当前迭代的数据，而是让当前迭代所需的数据由前一个迭代加载，这样它的计算就不会被数据加载阻塞(因为数据已经准备好了)。在进行计算时，它还加载将用于下一次迭代的数据。通过数据加载和计算的重叠，可以显著提高内存带宽和SM的利用率。我们将数据预取应用到矩阵A和b中。
如Alg. 4所示，我们使用数据预取设计我们的TSM2。在第4行和第5行，我们分配了两组t3寄存器来存储矩阵A元素的当前块和矩阵A元素的下一个块，用于预取。在第6行和第8行，我们分配t2寄存器的数据预取的元素在矩阵B,分配t2*t1存储当前加载的矩阵B, 注意我们不能在寄存器存储当前矩阵B,因为元素在矩阵B需要在计算线程间共享。
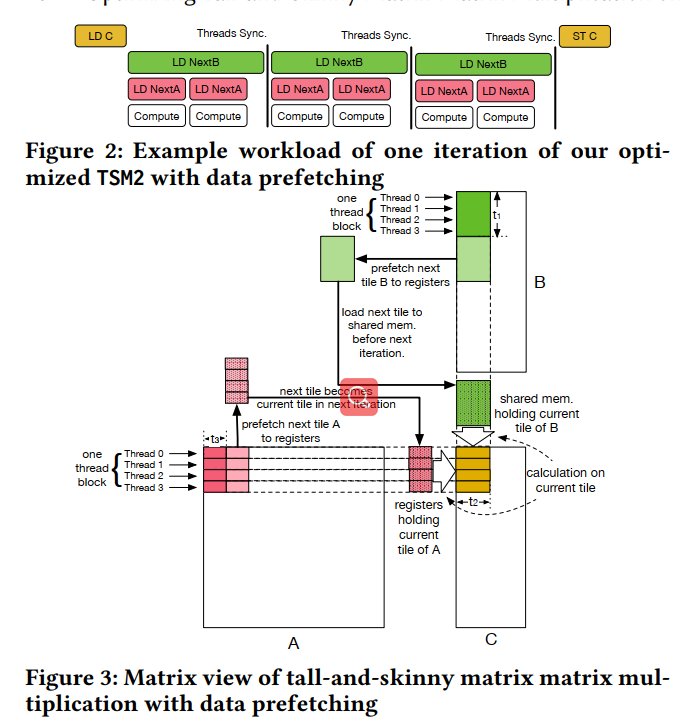
在核心计算迭代之前(第20-40行)，我们将矩阵A和B的当前块预加载到寄存器和共享内存中(第13-19行)，这样我们一进入计算循环，计算就可以立即开始，而不会受到任何数据依赖关系的阻碍。主要的计算在第28-30行。为了重叠计算和内存访问,我们在计算之前初始化下一行的加载(第21-23行矩阵B，第25-27行矩阵A)。我们使用两个循环载入矩阵A和B,因为我们想要为两个矩阵灵活地调整加载速度(tile size)。我们将在下一小节中讨论这个问题。图2和图3显示了使用数据预取的优化TSM2的一次迭代。LD C和ST C代表加载矩阵C初始值和将结果存储回矩阵C .每一次迭代，我们展示三个sub-iterations来载入矩阵B。我们在计算的同时加载下一个矩阵B的块(tile)来提高内存带宽利用率。在每次迭代结束时插入一个线程同步。对于最内部的迭代，我们每次都从矩阵A中进行实际计算和预加载元素。请注意，每个矩形的长度并不能准确地表示实际的执行时间长度，并且在实际计算中，LD nextA与LD nextB的数量之比不一定是2。此外，我们显示一个线程块与四个线程只是为了说明建议。我们将在下一小节中讨论，不同的参数值可以影响每个部件的长度以及LD nextA和LD nextB的数量之比。特别是LD nextA和Compute的执行时间，它会影响计算的特性(即内存限制或计算限制)。另外，为了简单起见，我们忽略了在这个figure中每个迭代的下一次块存储到当前块存储之间移动数据的部分。
3.6 参数定义
在Alg. 3和Alg. 4中，我们引入了三个可调参数:t1、t2和t3。在本节中，我们首先讨论每个参数如何控制TSM2的计算。然后，我们介绍我们的性能模型，该模型估计特定的性能指标如何随这些参数变化。最后，我们解释了我们的策略，选择这些参数的值，以实现高的GPU资源利用率和优化的整体性能。请注意以下讨论都是基于Alg. 4。
3.6.1参数行为
首先，我们将每个参数的行为如下：
\1. t1矩阵B的一个tile的行数，为了最大限度地利用可用的活动线程，并避免由于warp偏差而导致任何低效的线程执行, 我们让每个线程块中的所有线程参与获取矩阵B的元素。为了快速合并的全局内存访问,我们让每个线程获取一行,所以t1也是每个线程块的线程总数。另外，因为我们让n个线程参与计算，所以线程块的总数可以计算为: n/t1。
\2. t2指定了矩阵C中每个线程一次处理的元素数。它用于将整个工作负载划分为几个较小的工作负载，这些工作负载由每个线程迭代处理。更小的工作负载使每个线程的SM资源使用更少，这允许我们保持更高的SM占用。然而，划分工作负载意味着我们需要为每个小工作负载重复加载矩阵A。所以，这是一种交易。t2还影响了我们算法核心部分的总内存取数与计算操作的比例，这使得我们可以调整计算以适应计算或内存的限制(稍后将详细讨论)。
\3. t3指定了矩阵A中每个线程一次读取的元素数量。由于获取的元素彼此独立，因此可以在不阻塞彼此的情况下完成，因此可以使用t3调整内存加载并发性。
3.6.2性能指标估计
在本节中，我们将介绍基于参数的性能模型，该模型用于评估三个重要的性能指标:SM占用率、内存带宽利用率和计算能力利用率。这些估计将用于优化总体性能。
\1. 最大SM占用估算
根据这些参数，我们可以计算每个SM的最大占用率，即每个SM的最大活动线程数。(有些工作也使用了最多数量的warp，这与我们的作品相似。我们发现在我们的性能模型中使用max线程更一致。我们还选择线程块大小作为该值的被除数，以确保预期的线程数是活动的。)这种占用主要受最大硬件允许线程数(HW _MAX)和每个线程的片上内存利用率限制。我们首先计算每个线程使用的寄存器总数。由于nvcc编译器可以优化寄存器利用率，所以我们使用最大寄存器数来估计这个值。首先，CUDA初始设置使用的寄存器数量相对来说是固定的，我们将这个数量表示为c。我们通过在线分析获得它的数量。然后，我们需要两组t2寄存器来存储矩阵B的元素，用于下一次的tile抓取和当前的tile计算。请注意，虽然矩阵B的当前块存储在共享内存中，但它仍然需要被传输到寄存器中进行计算。接下来，我们需要t2寄存器来保存矩阵c的中间结果。最后，我们需要两组t3寄存器来存储矩阵A的元素，用于下一次磁片抓取和当前磁片计算。所以寄存器的总数是
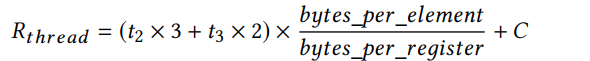
至于共享内存，通过为每个线程块分配共享内存，我们计算每个线程用于一致计算的平均共享内存数量。因为每个线程块分配的共享内存的大小是t1*t2，我们将在前面讨论设置t1 = threads_per_threadblock，所以平均分配给每个线程的共享内存是
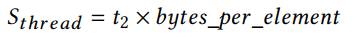
因此，最大SM占用率可以计算为:
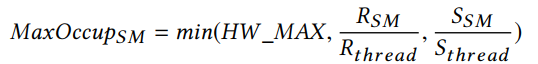
在上面的计算中，RSM和SSM表示每个SM的最大可用寄存器和共享内存。
\2. 估计最大内存带宽利用率
其次，我们估计当计算是内存限制时，我们的算法的最大内存带宽利用率。在这种情况下，在我们的算法中，加载矩阵A的元素占主导地位，而不是延迟点的计算。因此，我们可以使用每个SM的最大并发全局内存访问数来估计最大内存带宽利用率。它可以被计算为：
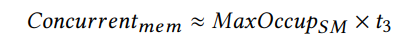
请注意，为了简单起见，我们这里只考虑对矩阵A的内存访问。由于大多数内存访问都是针对矩阵A的，因此这只会带来较小的不准确性。
然后，与[25,27]类似，我们使用Little ‘s Law计算每SM所需的最小并发内存访问数，以实现最大的内存带宽利用率:
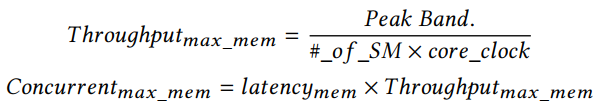
latencymem是平均的全局内存访问延迟，在我们的模型中，它被认为是一个常数，并且是通过在线proiling获得的。估计内存带宽利用率为:
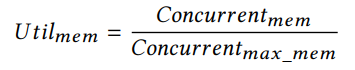
\3. 评估最大计算能力使用
然后，我们估计了计算限制时算法的最大计算能力利用率。在这种情况下，在我们的算法中，浮点数的计算占主导地位，而不是内存访问。因此，我们可以使用每个SM的最大并发浮点操作数来估计最大的计算能力利用率。可以计算为:
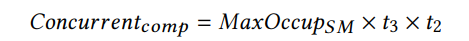
然后，与[25]相似，我们使用Little’s Law计算每SM需要的并发loating point操作的最少数量，以实现最大的计算能力利用：
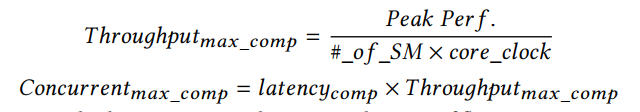
latencycomp是我们计算中的浮点操作的平均延迟，它在我们的模型中被认为是一个常数，是通过在线分析获得的。因此，估计的计算能力利用率为:
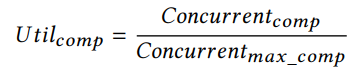
\4. 确定计算或内存界限
给定参数和规格GPU，我们可以确定当前的计算是内存还是计算限制。这主要是由Alg. 4的最内部循环(第24 - 34行)决定的。内存加载指令(第25-27行)与计算(第28- 30行)重叠。因为第31-33行取决于内存加载结果，所以它充当内存加载和计算的隐式同步点。这两部分所花费的时间将决定当前计算是计算限定还是内存限定。因此，我们首先估计计算和内存访问所需的时间如下：
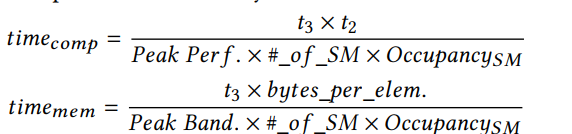
然后，通过比较这两种时间开销，我们可以确定当前的计算是计算限制还是内存限制。
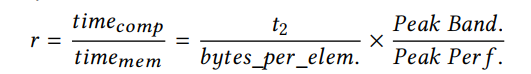
我们可以看到，当r大于1时，计算是计算界。否则，计算将受到内存限制。此外，由于我们使用t2将原始工作负载划分为几个较小的工作负载，因此这个比率由t2决定。通过调整t2，可以在计算和内存之间切换实际的计算。通过令r = 1计算两种情况的边界，得到t2的阈值:
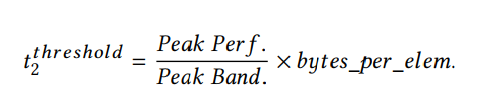
同样，我们也可以估计原始问题的计算特性，即工作负载没有被划分为更小的工作负载。在这种情况下，t2总是被赋给k，因此，通过比较k和t2threshold，我们可以估计出计算特性。如果k大于t2threshold，那么原来的问题是计算限制。否则，它是内存限制的。
很容易看出，根据t2和k的取值，可以看出当前问题和原问题的计算特性不同，从而影响整体性能。我们在下一节中讨论这个。
3.6.3选择参数
在选择参数时，我们首先要确定的是我们应该优化计算还是优化内存带宽。这取决于给定的GPU上给定的TSM2计算应该是计算还是内存的限制。在最后一节中，我们提出通过比较k和t2threshold来估计这个特性，这样我们就可以调整参数，使计算朝着正确的方向进行优化。
在原来的问题是内存限制(k <= t2threshold)的情况下，我们需要将实际计算也保持为内存限制(让1< t2 <k)，并优化内存带宽利用率。另一方面，如果原问题是计算限制(k >t2threshold)，我们首先尝试保持实际计算的计算限制(设t2threshold<=t2 <=k)，并优化计算功率的利用。然而，在给定GPU上的et2threshold过高的情况下，我们也尝试优化它的内存界限(让1< t2<t2threshold)，并输出性能更好的结果参数。
Alg. 5给出了t2和t3的参数优化过程。我们首先确定第一行的计算特性。如果是内存限制，我们将对从全局内存中访问所需元素的总时间成本进行优化(第4行)，否则，我们将对总计算时间(第9行)或内存访问时间(第14行)进行优化。请注意，为了简单起见，我们只计算访问矩阵A的内存访问总数，因为访问矩阵B的内存访问总数比访问矩阵A的内存访问总数少得多，所以这种简化只会带来较小的误差。此外，考虑到对矩阵B的总访问次数会带来一个额外的参数(t1)，这可能很难优化，因为t1也与线程组织有关，很难进行基于模型的估计。内存带宽利用率项(Utilmem)和计算能力利用率项(Utilcomp)是使用前面提到的公式计算的。由于我们的优化目标中有两个参数(t2和t3)，所以我们使用梯度下降(GD)进行优化。在GD中，根据我们的经验，我们将t2和t3的初始值都设置为1，步长设置为0.1。停止阈值设置为1e-4，因为我们不需要非常精确的精度。inal t2和t3四舍五入为最接近的整数。
为了优化t1，我们发现它只控制每个线程块中的线程数。由于线程的总数被固定为n，所以t1只决定这些线程是如何组织成线程的块。存在权衡:如果t1较大，那么对矩阵B中元素的总访问次数就会减少，但是，大的线程块意味着需要大量的线程参与相同的同步，这可能会对性能产生影响。另一方面，如果t1较小，则对矩阵B元素的总访问次数较高，但较小的线程块使调度更加灵活和有效。由于理论上难以确定t1的最优值，因此我们采用在线实验的方法来选择最优值。特别地，一旦确定了t2和t3，我们将基准测试不同的t1值，可以像前面提到的那样划分MaxOccupSM，并选择性能最好的t1。因为我们固定每个线程的共享内存数量 (Sthread = t2 bytes_per_element)，尽管t1似乎对共享内存分配(或最大SM占用)有直接影响，但实际上它对共享内存的影响有限。
4 实验
在我们的异构实验平台集群Darwin上对我们优化的TSM2进行了评估。
我们使用单GPU卡在一个GPU节点上运行每个测试。我们使用三种不同的微架构对三种常用的现代Nvidia gpu进行测试:Kepler、Maxwell和Pascal。
对于Kepler GPU，我们使用Tesla K40c，它有1430 GFLOPS峰值双精度性能和288 GB/s内存带宽。
对于Maxwell GPU，我们使用Tesla M40，它有213 GFLOPS峰值双精度性能和288 GB/s内存带宽。
对于Pascal GPU，我们使用Tesla P100，它有4600 GFLOPS峰值双精度性能和720 GB/s内存带宽。
我们使用CUDA C实现了TSM2的单点和双精度输入。为了更好地控制寄存器分配，我们禁用了编译器自动运行。为了进行比较，我们将TSM2与当前最新的cuBLAS 9.0库和最新的BLASX库[26]中的GEMM进行比较。
另外，我们尝试将我们的工作与KBLAS[8]进行比较，但是由于它的GEMM内核是基于cuBLAS的，所以它的性能与cuBLAS相同，所以我们省略了它的结果。每个测试重复多次，以减少误差和定时使用CUDA事件API。我们通过计算FAMD指令的性能来度量性能。我们还使用nvprof在命令行上测量全局内存吞吐量，并使用–metrics gld_throughput选项。
此外，我们使用–metrics gld_efficiency 选项来验证在我们的优化过程中实现了100%的全局内存访问效率(由于页面限制，我们省略了对效率验证结果的表示)。
4.1 实验环境
我们的输入矩阵是用随机的浮点数(0到1)初始化的。大输入矩阵的大小从10240∗10240到30720∗30720。瘦长的输入矩阵的大小范围从10240∗k到30730∗k，其中k等于2、4、8和16。
4.2 不同优化组合的测试
我们使用cuBLAS 9.0中的GEMM作为比较基线。
我们在TSM2中应用不同的优化组合，并与在cuBLAS和BLASX中的GEMM进行比较。
我们总共有四个版本的TSM2: V0: Alg. 1中描述的最简单的内积版本;
V1: Alg. 2中的外部产品版本。
该版本从算法级上减少了全局内存访问的总数;
V2:基于Alg. 2中的外部生产版本，我们增加了共享内存的使用，这使得对矩阵B的全局内存访问更加有效;
V3:基于Alg. 2中的外部产品版本和共享内存的使用，我们添加了数据预取。
这是我们优化实现的最佳版本，Alg. 4中对此进行了描述。
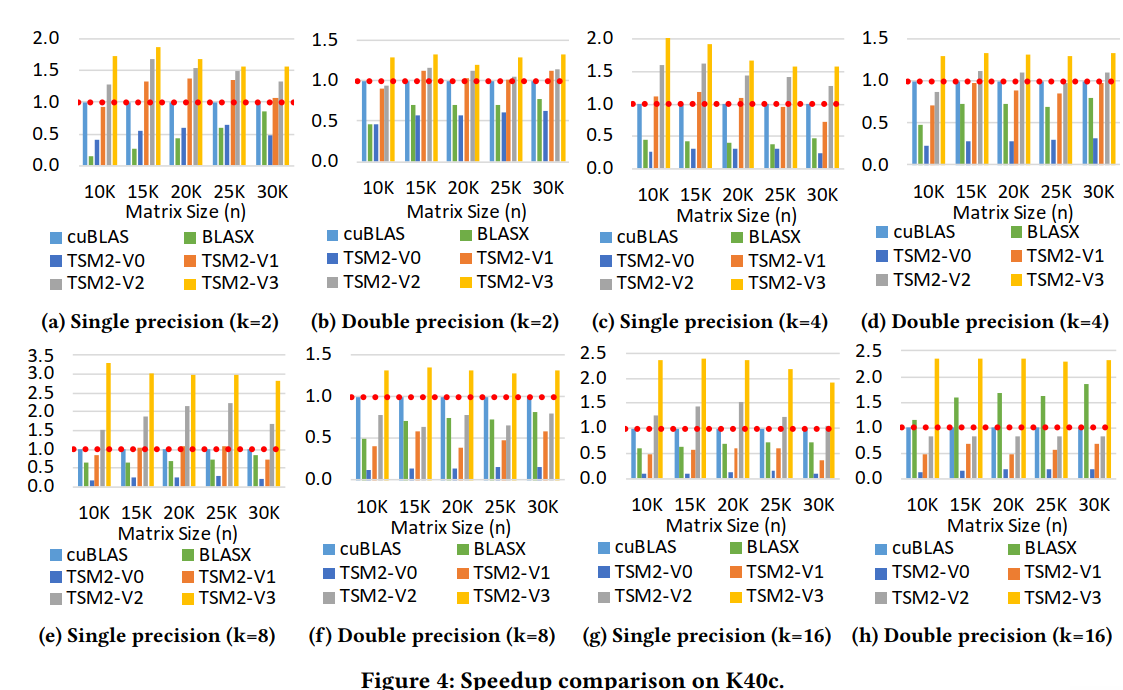
由于页面空间的限制，我们只在K40c GPU上显示结果。我们的优化在其他gpu上也有类似的表现。为了评估我们的优化，我们需要确定我们的程序是由哪个资源限制的。由于t2threshold (k40c) 40，对于给定的k值，计算总是内存限制的。优化参数为:t2 = k, t3 = 4, t1 = 128。这些参数只适用于最后的TSM2版本。图4显示了不同版本在单精度和双精度下的加速效果。从结果中，我们可以看到TSM2-V0的性能非常差，这是因为在内部积版本中需要更多的全局内存访问。
另一方面，TSM2-V1与TSM2-V0(快2.2倍- 4.7倍)相比，显著提高了性能，因为它需要更少的全局内存访问次数。TSM2-V2进一步提高了对矩阵B的全局内存访问的效率，这对整体性能起着至关重要的作用。此外，在一个线程块内的线程之间共享矩阵B的块也减少了对矩阵B的总内存访问次数，这导致了额外的1.1x到2.1x的加速。最后，TSM2-V3中引入的数据预取进一步缓解了内存访问瓶颈，从而带来了额外的1.3倍- 3.5倍的加速。
4.3内存吞吐量分析
图5显示了K40c GPU上TSM2-V3、cuBLAS和BLASX单精度和双精度的内存吞吐量。结果表明，与cuBLAS相比，TSM2的GPU内存带宽利用率提高了12.5% - 26.6%(平均17.6%)，与BLASX相比提高了20.1% - 38.8%(平均24.3%)。
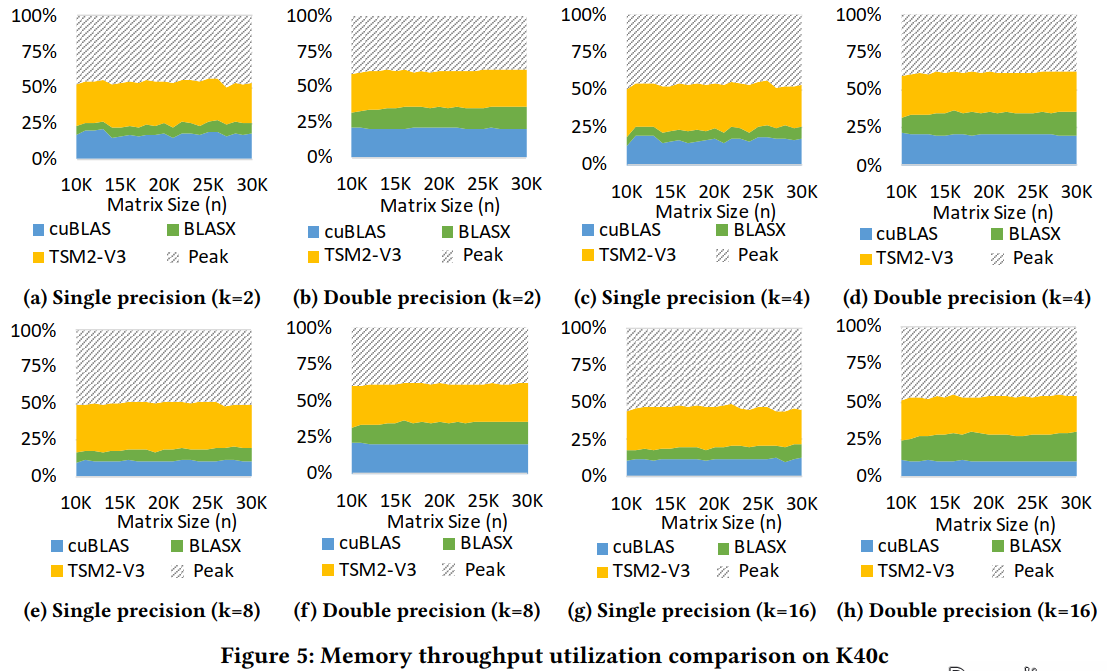
4.4不同微处理机架构测试
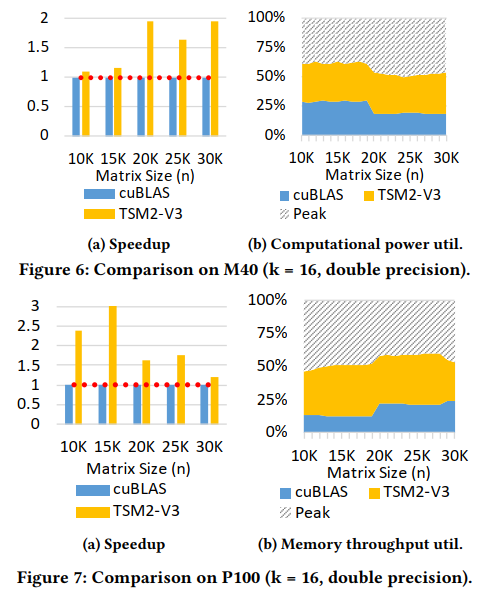
除了开普勒微结构，我们还进行了新的马克斯韦尔和帕斯卡gpu的测试。与Kelper GPU类似，我们得到t2threshold (m40) 6和t2threshold (p100) 50 Tesla m40具有较慢的计算能力，因此k = 16时的输入计算是计算限制。我们的参数优化过程也输出有利于计算优化的参数:t2 = 8, t3 = 4, t1 = 256。如图6所示，我们的优化实现在Tesla M40上实现了1.1x -1.9x (avg. 1.47x)加速，与cuBLAS 9.0中的GEMM函数相比，计算功耗提高了7%到37.3% (avg. 20.5%)。因为P100有更强的计算能力，我们可以看到k = 16时的计算是受内存限制的。我们的参数优化过程也输出有利于内存优化的参数:t2 = 4, t3 = 4, t1 = 128。如图7所示，我们的优化实现在Tesla P100上实现了1.1x - 3.0x(平均2.15x)的加速，与cuBLAS中的GEMM函数相比，内存带宽利用率提高了17%到47.6%(平均34.7%)
5 展示
在本节中，我们将使用两个真实的应用程序来展示TSM2带来的性能优势。
5.1 K-means
经典的Lloyd K-means算法是大数据分析中最常用的聚类方法之一。
它的核心计算是计算每个数据点与每个质心之间的距离。
下面是计算这个距离的优化方法。
首先，可以通过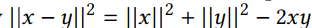 
来计算数据点x与质心y之间距离的平方。
然后，通过将所有计算聚集在一起，我们可以使用更多有效的向量向量乘法(||x ||2 + ||y||2)和GEMM (xy)。
这种优化被广泛应用于经典的Lloyd s K-means算法在gpu和cpu上的最新实现中。例如，Nvidia[1]提供的实现使用cuBLAS GEMM例程计算距离(即计算xy)。当质心的数目很小时，这个计算就变得瘦高型(n×d by d×k, n是数据点的数目，k是质心的数目，d是每个数据点和质心的维数)。与计算||x ||2和||y||2相比，计算xy占用了(O(d(n + k)) vs. O(ndk))的大部分计算时间，因此其性能对整个算法至关重要。
在这里，我们将[1]中的GEMM例程替换为我们的TSM2。我们设置质心数量k = 16，数据点维数d = 4096，并将数据点n的数量从1k改为262k。每个数据点的每个维数都是随机生成的双loating点，范围从0到1.我们比较了irst 100迭代的执行时间。结果如图8所示。使用我们的TSM2，我们在Nvidia Tesla K40c上加速K-means 1.06x - 1.89x(平均1.53x)。
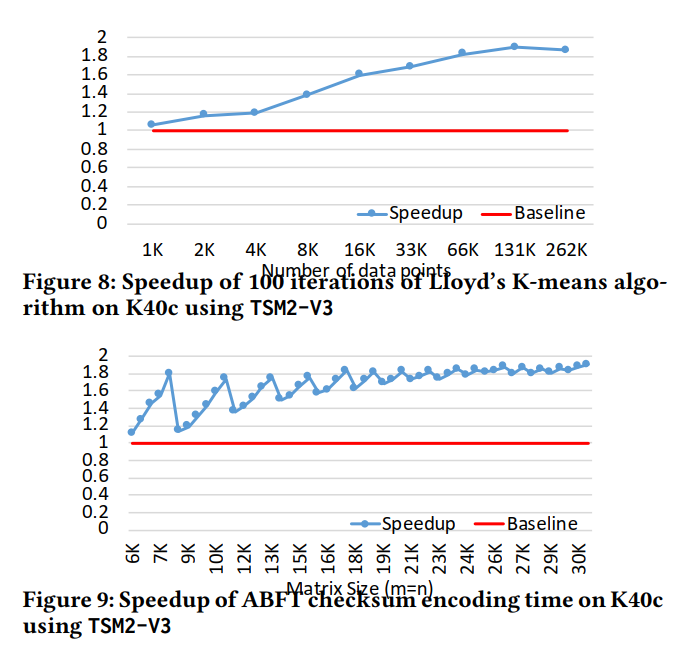
5.2 ABFT矩阵校验和编码
矩阵校验和编码是ABFT中最重要的运算之一[10,11,22,28,30]。
它的计算包括让一个矩阵(或更高编码密度的矩阵块)乘以一系列预先定义的向量，从而得到矩阵行或列的加权和。通常的选择是使用两个向量。当把这两个向量组合在一起时，计算就变成了一个瘦高的矩阵-矩阵乘法。GPU上最常见的选择是使用cuBLAS。在这里，我们通过使用cuBLAS和我们的TSM2来比较校验和编码性能。结果如图9所示。正如我们所看到的，我们的TSM2在Nvidia Tesla K40c上显著地将校验和编码计算从1.10x提高到1.90x加速(avg. 1.67x)。我们注意到当矩阵很小的时候会出现加速振荡的情况。这主要是由于负载平衡的变化，因为不同的输入矩阵大小是给定的。我们将在以后的工作中对此进行优化。
6 结论
在这项工作中，我们首先分析了当前的GEMM在最新cuBLAS库中的性能。
我们发现，当输入形状是瘦高型的，当前的实现缺乏充分利用的计算能力或内存带宽。然后，我们发现了优化tall-and-skinny GEMM的潜在挑战，因为它的工作负载可能在计算绑定和内存绑定之间变化。接下来，我们重新设计了一个优化的瘦高的GEMM与几个优化技术集中在GPU资源的利用。最后，实验结果表明，我们的优化实现可以在三种现代GPU微架构上实现1.1x -3倍的加速。