k-means聚类算法

随机生成K个聚类中心

迭代以下操作，直至聚类中心不在移动，训练集的标签不再改变
簇分配
移动聚类中心

不易分离簇

优化目标

J 也叫失真函数，畸变函数

14优化目标

随机初始化

使得算法避免局部最优解

随机初始化状态不同，导致结果也不同，可能得到不好的局部最优。

使用多次随机初始化找到使得 J 最小的聚类中心

14多次随机初始化

选取聚类数量

（1）手动选择

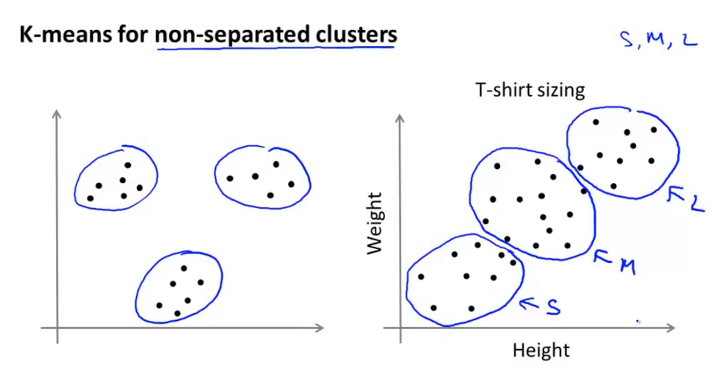
可视化数据，观察数据分离情况

（2）“肘部法则”

分别K = 1，2，3，4，5… 绘制 J 的曲线，选择拐点。但是有时很模糊~

（3）接下来数据的分类情况做一个评估

编程作业

pca.m

function [U, S] = pca(X)
%PCA Run principal component analysis on the dataset X
%   [U, S, X] = pca(X) computes eigenvectors of the covariance matrix of X
%   Returns the eigenvectors U, the eigenvalues (on diagonal) in S
%

% Useful values
[m, n] = size(X);

% You need to return the following variables correctly.
U = zeros(n);
S = zeros(n);

% ====================== YOUR CODE HERE ======================
% Instructions: You should first compute the covariance matrix. Then, you
%               should use the "svd" function to compute the eigenvectors
%               and eigenvalues of the covariance matrix. 
%
% Note: When computing the covariance matrix, remember to divide by m (the
%       number of examples).
%
sigma = X' * X / m;
[U,S,v] = svd(sigma);
% =========================================================================

end

projectData.m

function Z = projectData(X, U, K)
%PROJECTDATA Computes the reduced data representation when projecting only 
%on to the top k eigenvectors
%   Z = projectData(X, U, K) computes the projection of 
%   the normalized inputs X into the reduced dimensional space spanned by
%   the first K columns of U. It returns the projected examples in Z.
%

% You need to return the following variables correctly.
Z = zeros(size(X, 1), K);

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the projection of the data using only the top K 
%               eigenvectors in U (first K columns). 
%               For the i-th example X(i,:), the projection on to the k-th 
%               eigenvector is given as follows:
%                    x = X(i, :)';
%                    projection_k = x' * U(:, k);
%

U_redeuce = U(:,1:K);
Z =  X  * U_redeuce;


% =============================================================

end

recoverData.m

function X_rec = recoverData(Z, U, K)
%RECOVERDATA Recovers an approximation of the original data when using the 
%projected data
%   X_rec = RECOVERDATA(Z, U, K) recovers an approximation the 
%   original data that has been reduced to K dimensions. It returns the
%   approximate reconstruction in X_rec.
%

% You need to return the following variables correctly.
X_rec = zeros(size(Z, 1), size(U, 1));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the approximation of the data by projecting back
%               onto the original space using the top K eigenvectors in U.
%
%               For the i-th example Z(i,:), the (approximate)
%               recovered data for dimension j is given as follows:
%                    v = Z(i, :)';
%                    recovered_j = v' * U(j, 1:K)';
%
%               Notice that U(j, 1:K) is a row vector.
%               

X_rec = Z * U(:,1:K)';

% =============================================================

end

findClosestCentroids.m

function idx = findClosestCentroids(X, centroids)
%FINDCLOSESTCENTROIDS computes the centroid memberships for every example
%   idx = FINDCLOSESTCENTROIDS (X, centroids) returns the closest centroids
%   in idx for a dataset X where each row is a single example. idx = m x 1 
%   vector of centroid assignments (i.e. each entry in range [1..K])
%

% Set K
K = size(centroids, 1);

% You need to return the following variables correctly.
idx = zeros(size(X,1), 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Go over every example, find its closest centroid, and store
%               the index inside idx at the appropriate location.
%               Concretely, idx(i) should contain the index of the centroid
%               closest to example i. Hence, it should be a value in the 
%               range 1..K
%
% Note: You can use a for-loop over the examples to compute this.
%


for i = 1:size(X,1)
  min_dis = Inf;
  for j = 1:K
     a  = X(i,:) - centroids(j,:);  
     dis  = sum(a.^2);
     if min_dis > dis
        idx(i) = j;
        min_dis = dis; 
     endif
   endfor
endfor

%else methods
%for i = 1 : size(X, 1)
%    for j = 1 : K
%    dis(j) = sum((centroids(j, :) - X(i, :)) .^ 2, 2);
%    end
%    [t, idx(i)] = min(dis);    %t存储的最小值， idx存储的最小值的索引
%end
 

% =============================================================

end

computeCentroids.m

function centroids = computeCentroids(X, idx, K)
%COMPUTECENTROIDS returns the new centroids by computing the means of the 
%data points assigned to each centroid.
%   centroids = COMPUTECENTROIDS(X, idx, K) returns the new centroids by 
%   computing the means of the data points assigned to each centroid. It is
%   given a dataset X where each row is a single data point, a vector
%   idx of centroid assignments (i.e. each entry in range [1..K]) for each
%   example, and K, the number of centroids. You should return a matrix
%   centroids, where each row of centroids is the mean of the data points
%   assigned to it.
%

% Useful variables
[m n] = size(X);  %300,2

% You need to return the following variables correctly.
centroids = zeros(K, n); %3,2


% ====================== YOUR CODE HERE ======================
% Instructions: Go over every centroid and compute mean of all points that
%               belong to it. Concretely, the row vector centroids(i, :)
%               should contain the mean of the data points assigned to
%               centroid i.
%
% Note: You can use a for-loop over the centroids to compute this.
%

for i = 1:m
  for j= 1:n
     centroids(idx(i),j) = centroids(idx(i),j) + X(i,j);
  endfor
endfor

for i = 1 : K
   id = (idx ==i);
   centroids(i,:) =  centroids(i,:)./sum(id);
endfor

%else methods（vectorized）
%for i = 1 : K
%     centroids(i, :) = (X' * (idx == i)) / sum(idx == i);    
     %(idx ==i)目的是将不是i值的X中对应数据变为0.
% end
% =============================================================
end

kMeansInitCentroids.m

function centroids = kMeansInitCentroids(X, K)
%KMEANSINITCENTROIDS This function initializes K centroids that are to be 
%used in K-Means on the dataset X
%   centroids = KMEANSINITCENTROIDS(X, K) returns K initial centroids to be
%   used with the K-Means on the dataset X
%

% You should return this values correctly
centroids = zeros(K, size(X, 2));

% ====================== YOUR CODE HERE ======================
% Instructions: You should set centroids to randomly chosen examples from
%               the dataset X
%

% Randomly reorder the indices of examples
randidx = randperm(size(X, 1));
% Take the first K examples as centroids
centroids = X(randidx(1:K), :);

% =============================================================

end