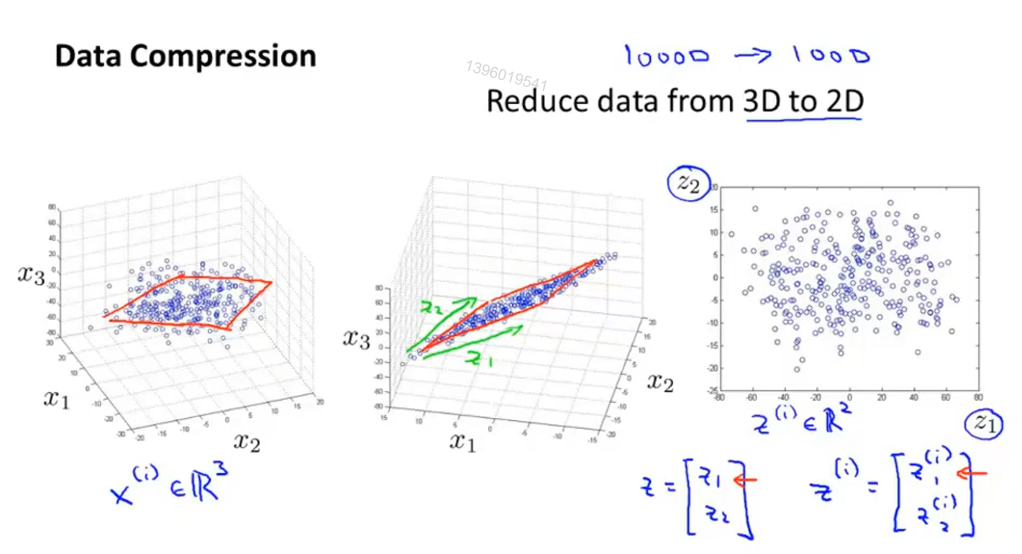
降维
运用于数据压缩,减少冗余
运用于可视化,抓住关键数据,绘制2D、3D图像
#
高维特征的问题:
• 存在大量冗余的特征,降低了机器学习的性能
• 数据可视化问题
• 数据处理的维度灾难
降维的目的:
• 发掘高维数据的内在维度,得到更紧凑(低维)的数据表达
内在维度
内在维度:表征数据变化的自由变量的个数
线性降维:关于内在维度的线性子空间的降维问题
非线性降维:非线性子空间(流形)
线性降维
将d维的原始数据线性投影到𝑑′维子空间
• 通常 𝑑′ ≪ 𝑑
𝑑′维子空间(投影矩阵)的选择取决于任务的要求
有监督的降维
降维要求:
• 降维后的不同类别数据之间的差别最大化
LDA算法(Linear Discriminative Analysis):
• 最大化 类别间散度(scatter)与类别内散度的比值
无监督的降维
特点:数据没有类别标签
要求: 降维后保留尽可能多的原始数据的信息
PAC(主成分分析 )
principal components analysis 不是线性回归
PAC 是找到低维子空间(正交子空间 )来对数据进行投影(对所有 x一 视同仁,没有 y)以便最小化投影误差的平方,也就是min(点与投影后的点之间的距离)
老师版教学过程
最近重构性
数据样本到投影点的距离最近



最大可分性
数据样本的投影点之间尽可能分开

PCA的优化方法

算法过程

吴恩达版教学过程
数据预处理
(1)特征放缩
(2)均值标准化
计算过程
Σ(大写的σ,不是求和符号)
(奇异值分解)svd( )数值上更稳定 再进行协方差计算时 结果等于 eig( )
z是降维后的U ,整个过程就是最小的平方投影误差 (数学证明复杂)

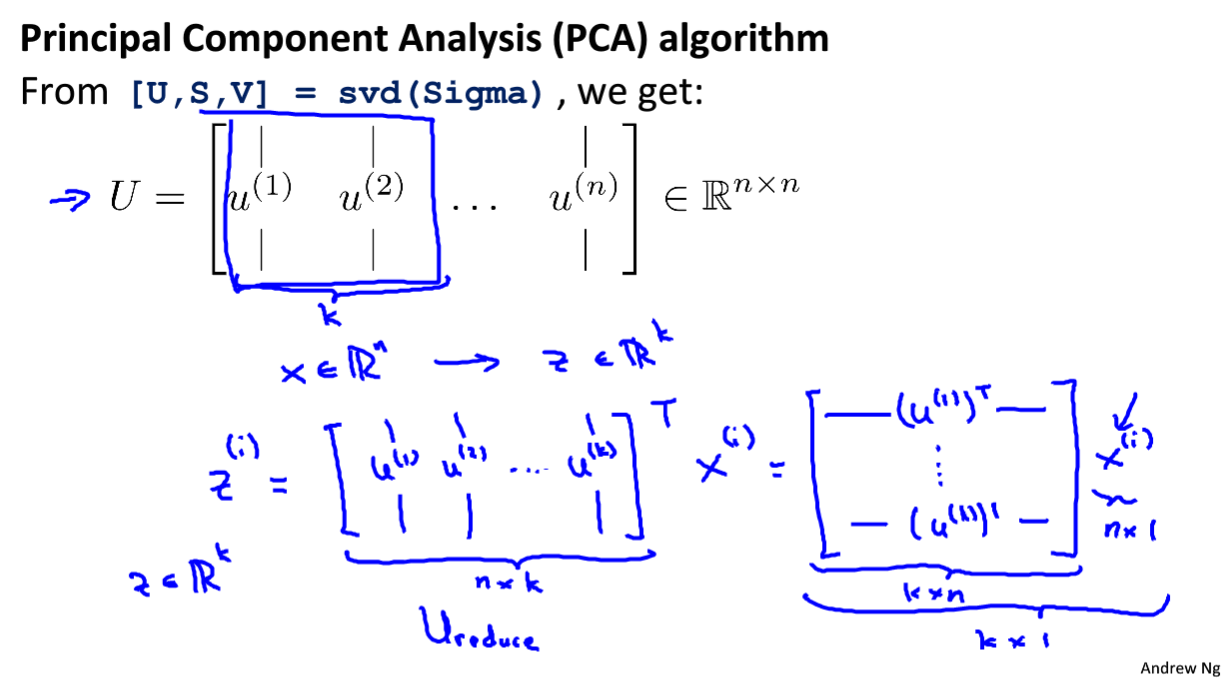

主成分数量的选择



压缩重现
得到压缩前数据的估计值
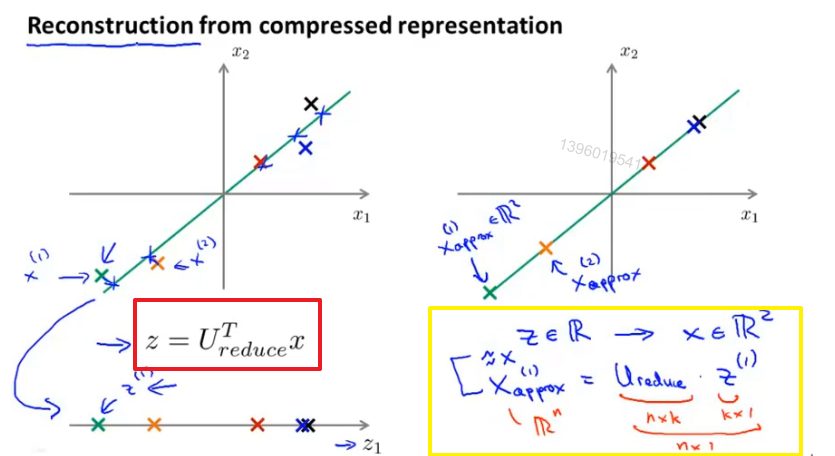
应用建议
(1)给监督算法加速
训练集利用PCA 建立 X 到 z 的映射,分类精度不会受影响

(2)错误用法 :防止过拟合
因为PCA丢掉了一些关键信息
(3)错误用法 :设计机器学习系统时 不比较 使用PCA和不使用PCA的情况
线性降维的不足
• 线性降维基于欧式距离
• 欧式距离无法应用于非线性子空间(流形)
非线性降维
“流形”是在局部与欧氏空间同胚(等价)的空间,形象的说法:“一块可弯曲的橡皮擦”。换言之,它在局部具有欧氏空间的性质,在局部才能用欧氏距离来进行距离计算。
“流形学习”是一类对分布在流形上的数据样本进行非线性降维的方法。
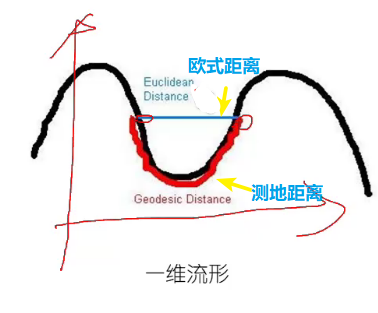
测地距离(Geodesic Distance)
• 测地距离衡量了流形(弯曲表面)上两点之间的最短距离
• 测地距离可以由两点之间的邻近点构成的最短路径来近似
等度量映射(ISOMAP)
目标:降维后的样本保持原样本空间的测地距离
方法:基于测地距离的“多维缩放” (MDS)
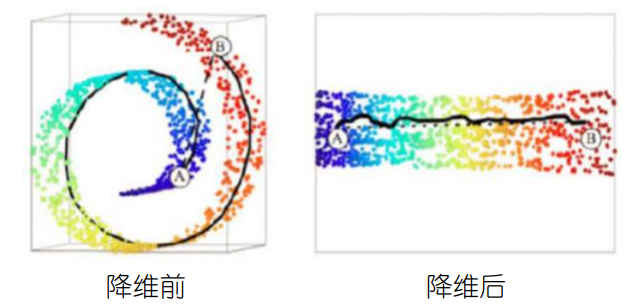
核心步骤:
- 计算任意两样本之间的测地距离(最短路径算法,例如: Djikstar算法)
- 以所有样本间的测地距离矩阵作为输入,调用MDS算法

多维缩放(MDS: Multi-dimensional Scaling)
假定有m个样本,在原始空间中的距离矩阵为D ,其第i行j列的元素dist_i_j 为样本 X_i到 _j的距离。
目标: 在低维空间中保持原始数据样本之间的欧式距离
MDS的求解方法
