VS2017
注释: 先CTRL+K,然后CTRL+C
取消注释: 先CTRL+K,然后CTRL+U
图形应用
计算机辅助设计(CAD:computer-aided design)
虚拟现实环境(virtual-reality environment)
科学计算可视化(scientific visualization)
未来发展
表情与动作的精细化
图形学与深度学习的碰撞
阴极射线管(CRT)
发光二极管显示器(LED:Liquid-emtting diode)
GPU 擅长于计算

像素:由图像的小方格组成的,这些小方块都有一个明确的位置和被分配的色彩数值,小方格颜色和位置就决定该图像所呈现出来的样子
显示分辨率:水平像素数*垂直像素数 ,取决于光点与帧缓存(存放一帧的信息)的大小
帧缓存的容量 = 分辨率 * 颜色位面数

可编程渲染管线
发展历程
固定管线:程序员控制权减少,不灵活

可编程图形库:自由搭建,功能范围广
从固定到可编程:hooks()函数(钩函数)突破固定功能流水线的限制,使用可编程着色器修改
流水线中特定步骤的行为。
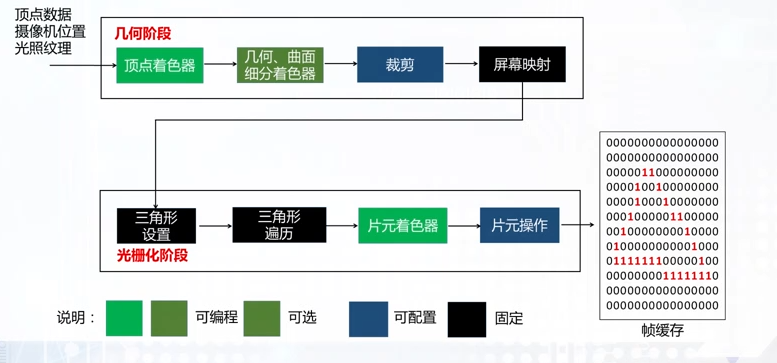
GPU渲染管线
应用阶段 -》 几何阶段 -》光栅化
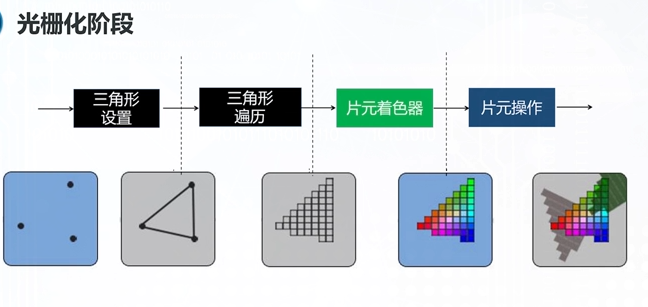
软光栅
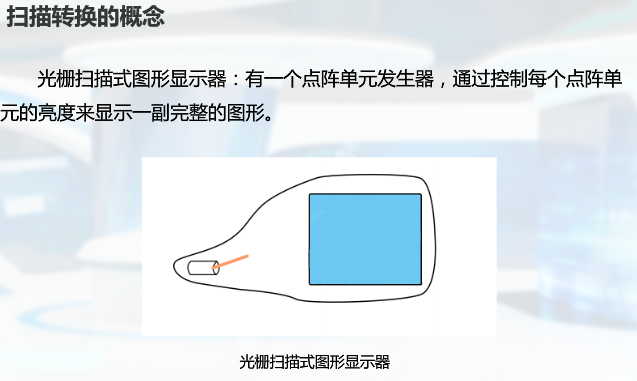
扫描转换也就是光栅化,点阵单元是像素点阵
图源经过算法计算(不借助硬件提供的api)转换成像素点

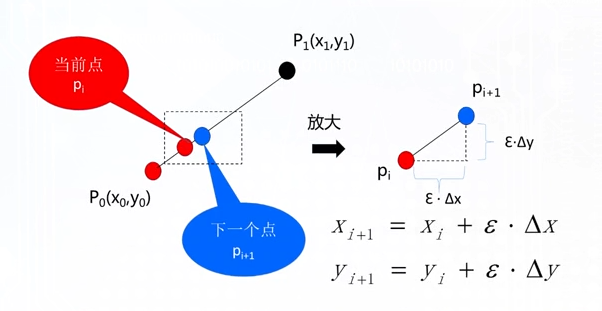
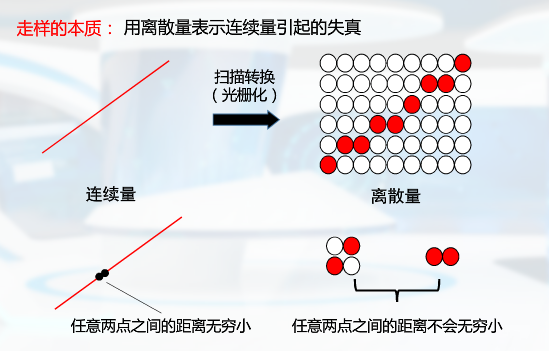
逼近的本质相当于 连续量向离散量的转换

直线扫描转换算法
逐点比较法、正负法、数值微分算法、Bresenham算法
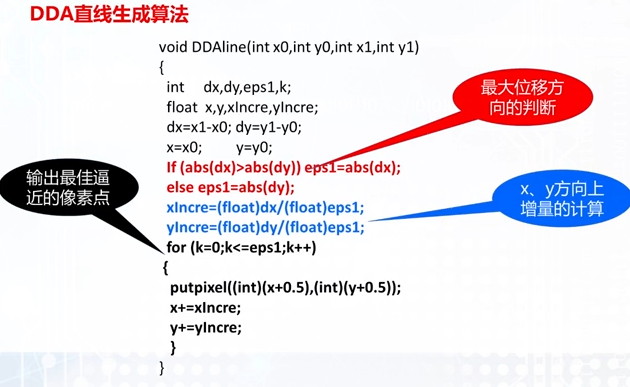
数值微分算法(DDA)


DDA是增量算法,优点:简单直观易实现,缺点:有浮点数和浮点运算,效率不高
记得取整(光栅化过程中不可能绘制半个像素点)
源码实现:
Bresenham算法
(1)中点

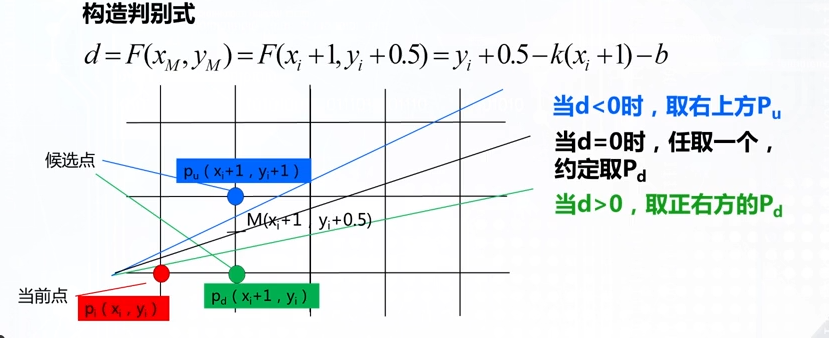
算法步骤:
假定0<k<1,x是最大位移方向;为防止浮点数出现,d(误差项)放大2倍

(2)改进

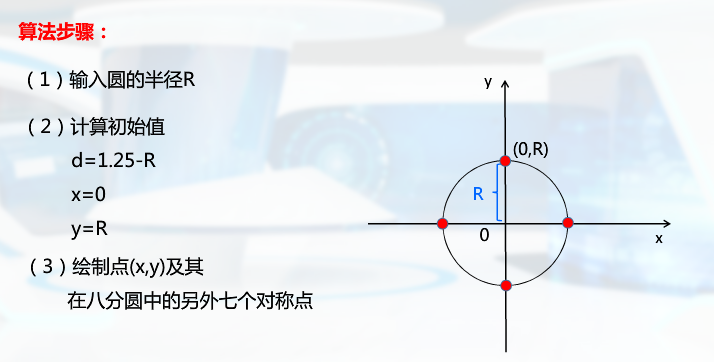
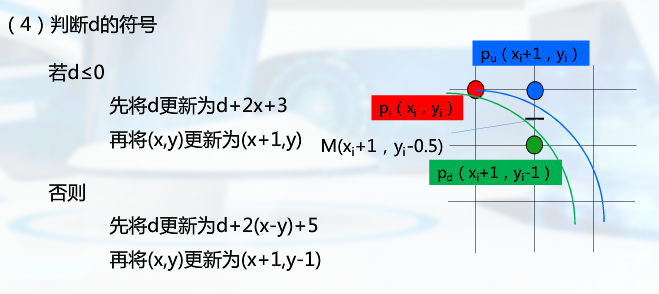
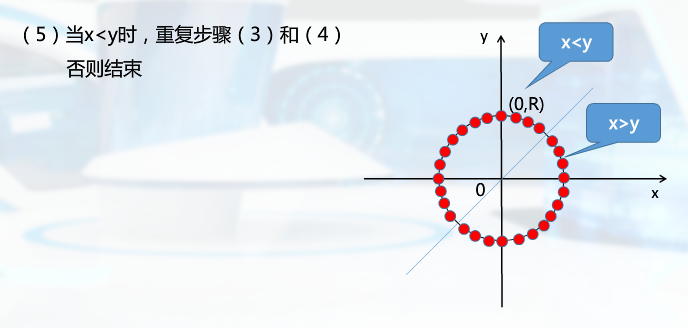
圆的扫描转换算法

常规计算太复杂
Bresenham算法
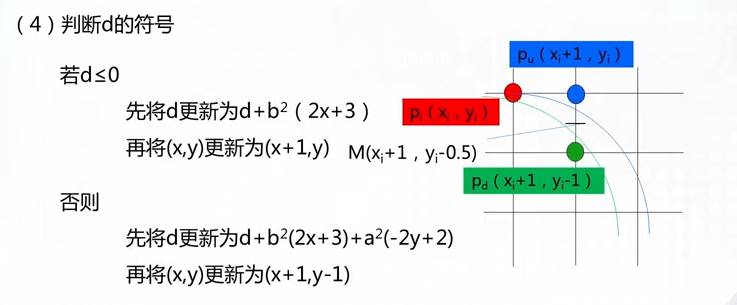
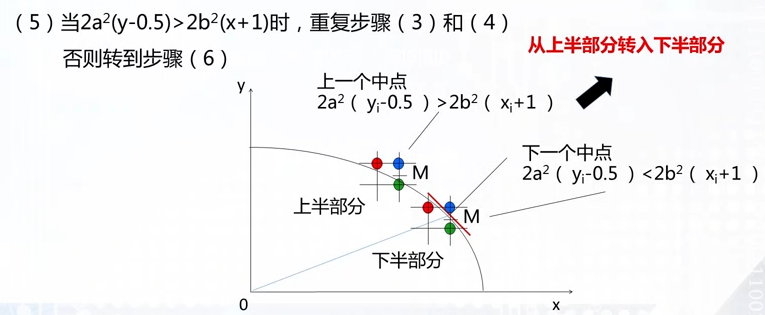
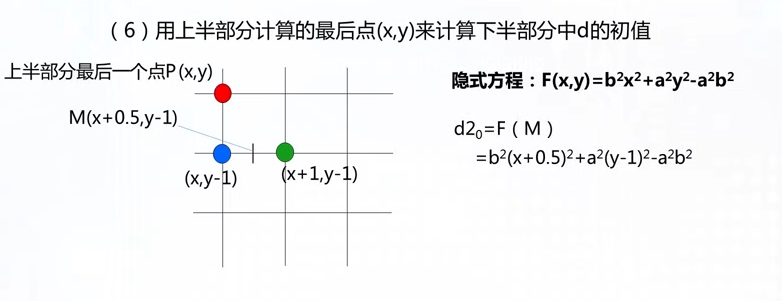
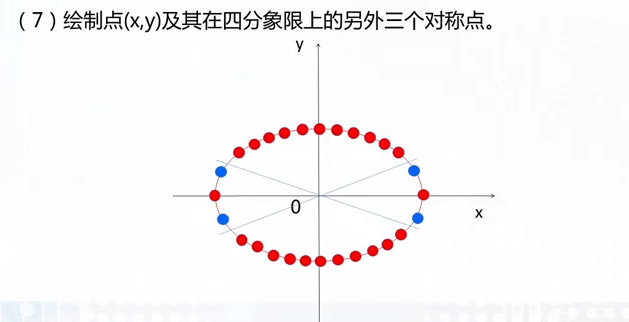
椭圆的扫描转换算法
在椭圆弧的扫描转换算法中,如果考虑的是中心在原点,第一象限的1/4段椭圆弧,则上下部分的分界点是椭圆弧上法向量x、y两个分量相等的点



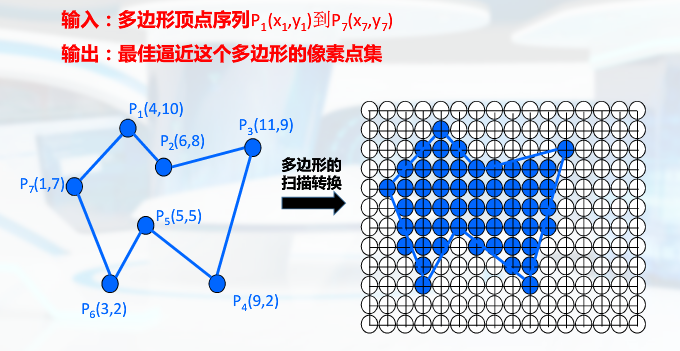
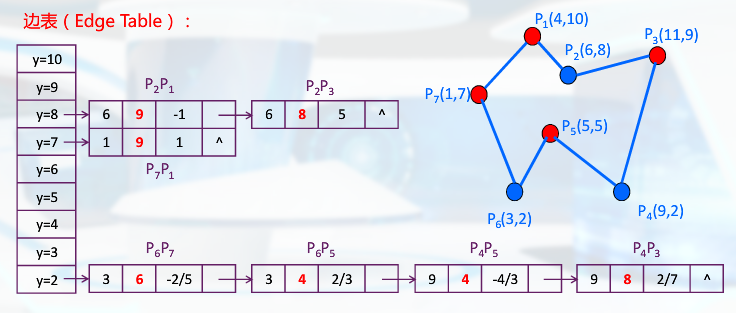
多边形的扫描转换算法
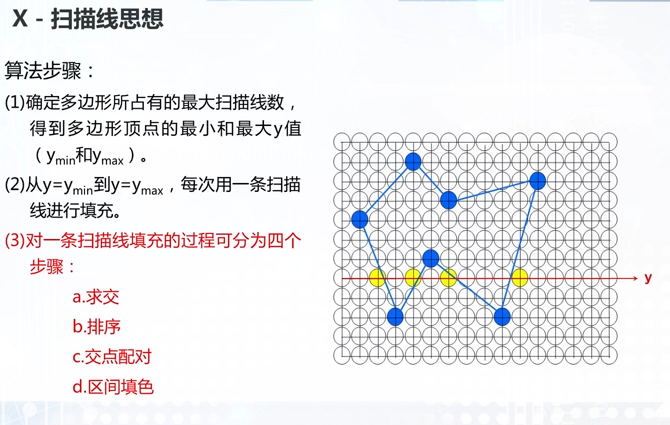
X-扫描线思想
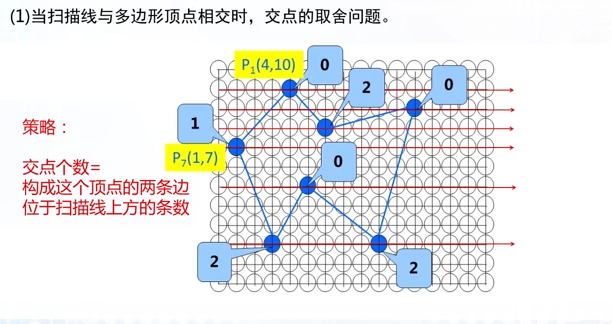
由于像素点较小,因此中心偏移看不出来
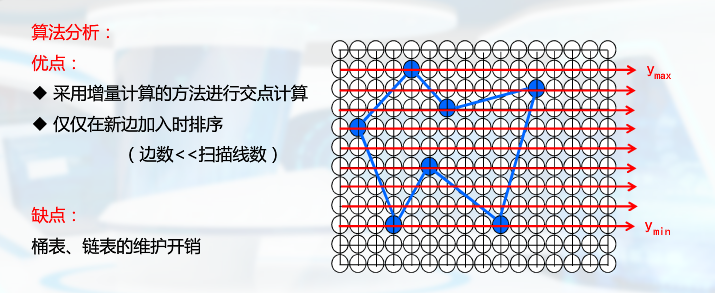
算法效率问题
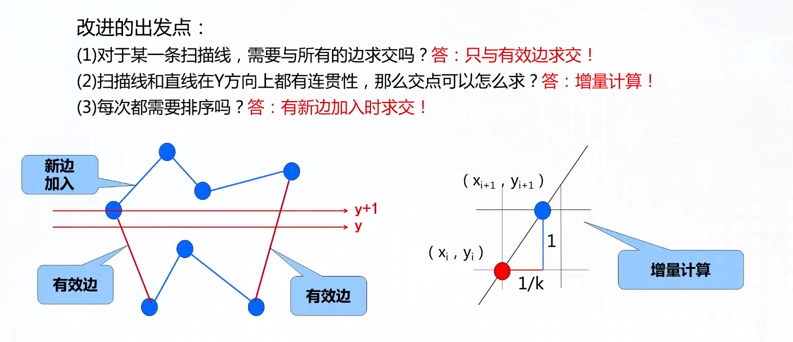
Y向连贯性算法
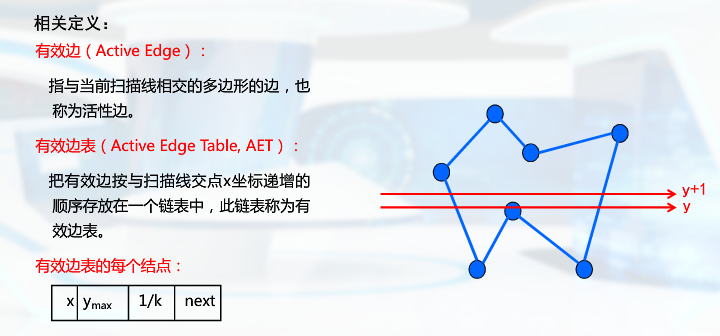
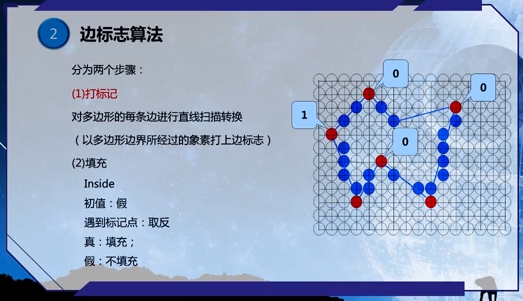
边标志算法
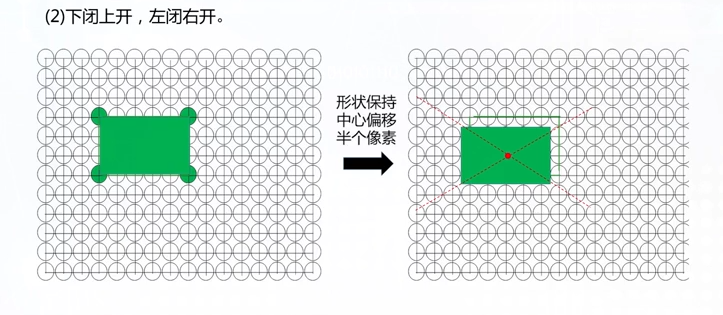
上闭下开


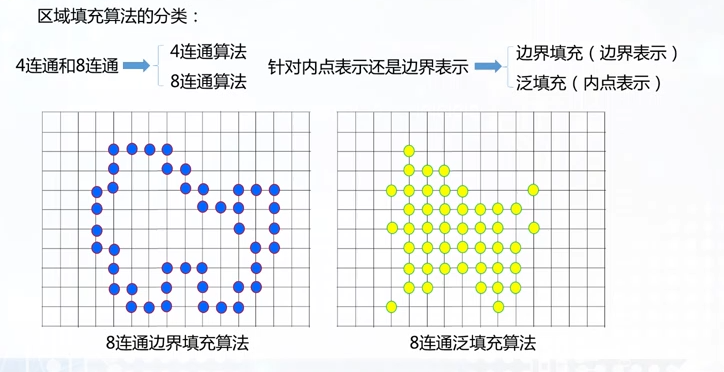
区域填充

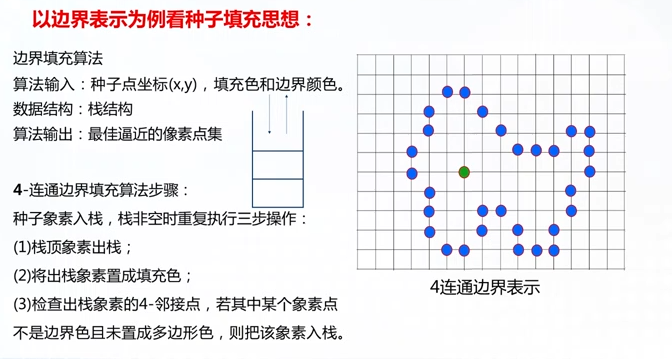
边界填充算法
8连通边界算法不可以填充4连通边界表示区域
泛填充算法通常用于给区域重新着色
8连通泛填充算法可以填充4泛填充的内点表示区域
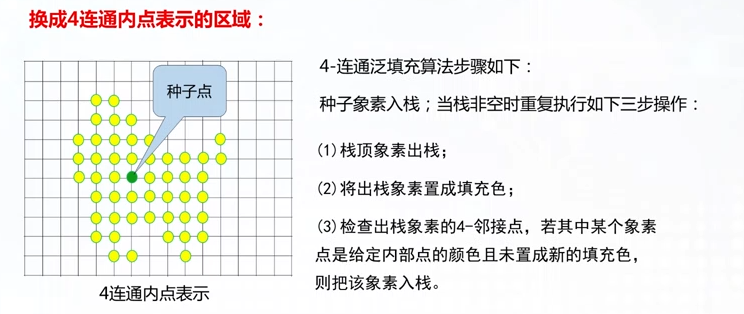
重复入栈问题
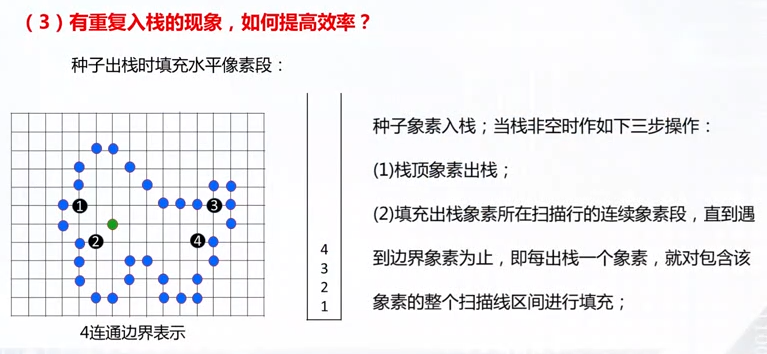

属性
颜色,虚实,宽细,纹理贴图
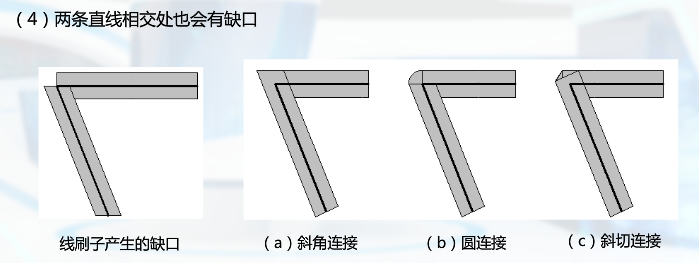
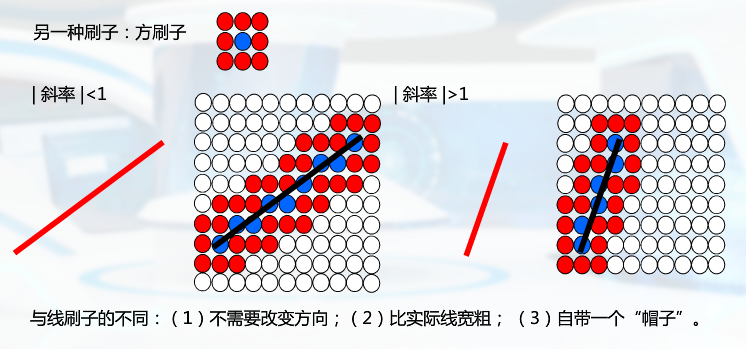
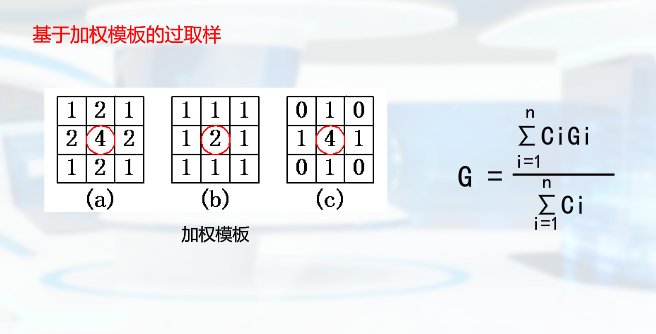
根据斜率改变模板
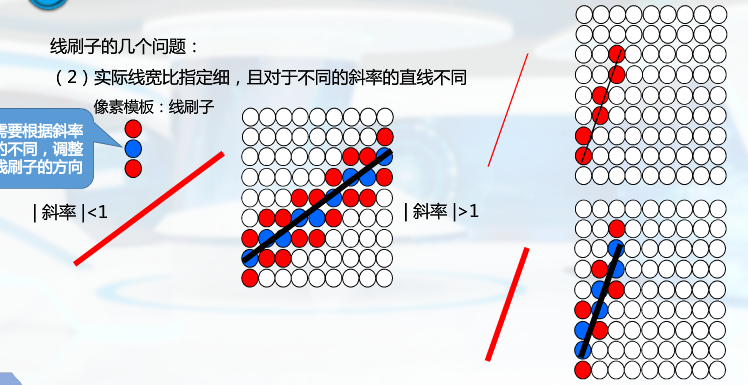
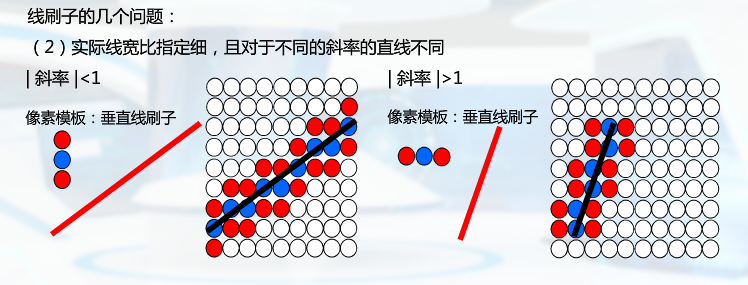
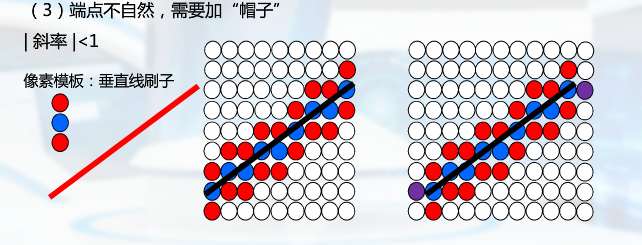
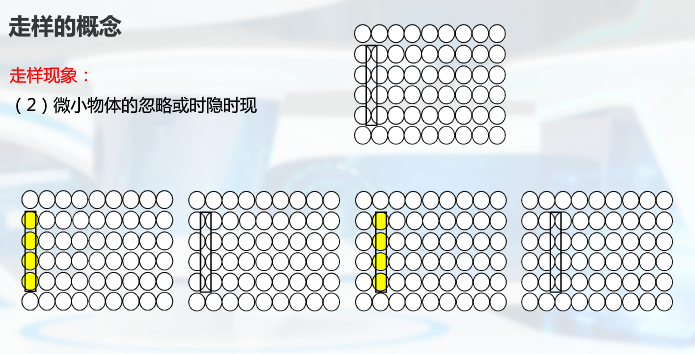
走样与反走样
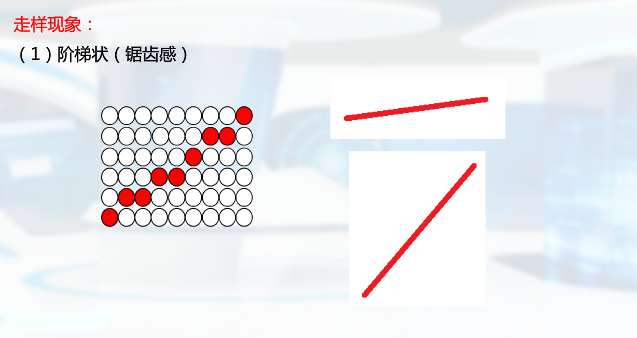
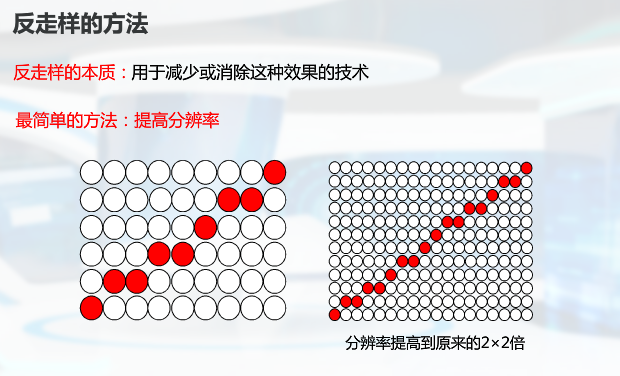
为提高图片质量,进行反走样

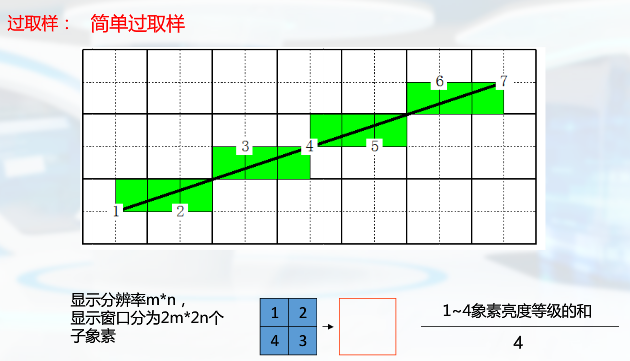
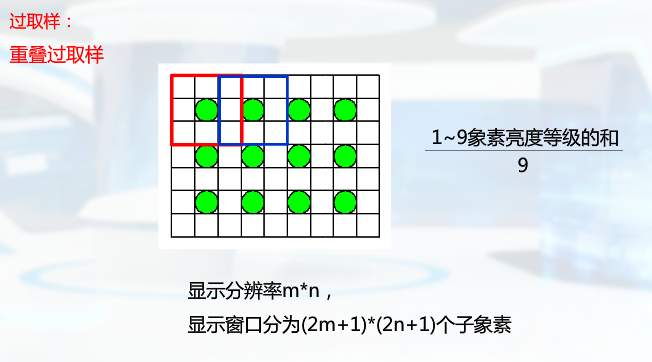
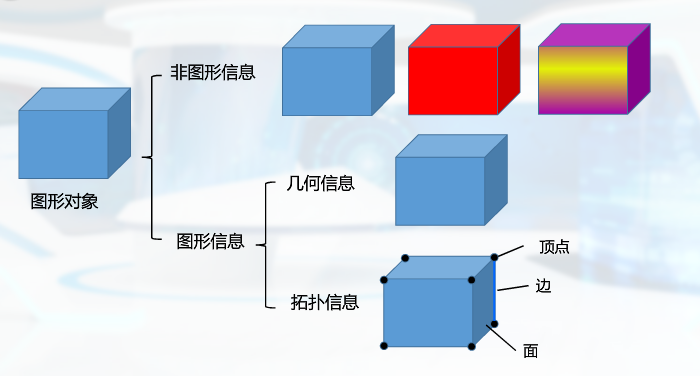
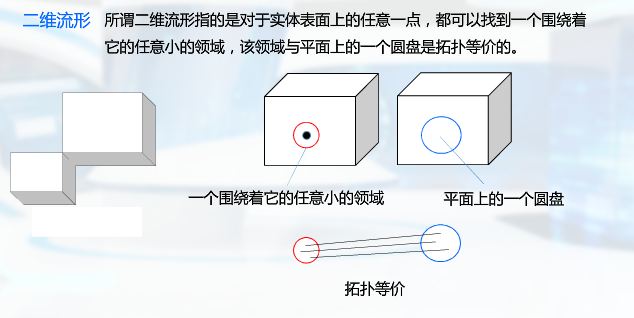
造型技术
研究如何在计算机中建立恰当的模型表示不同图形对象的技术
对象:规则对象(几何模型)、不规则对象(不能用欧式几何加以描述的对象如山树云烟)



实体



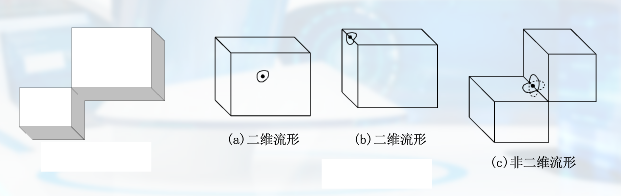

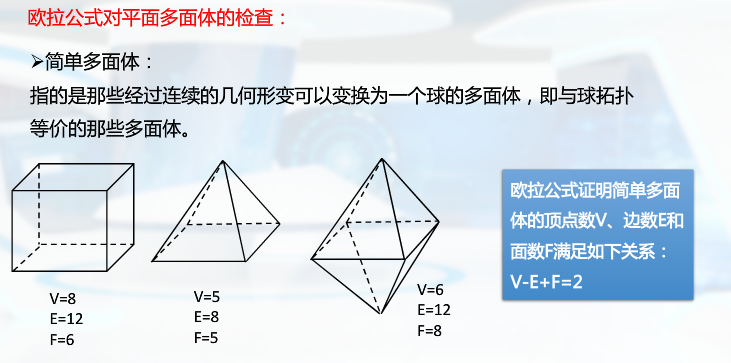
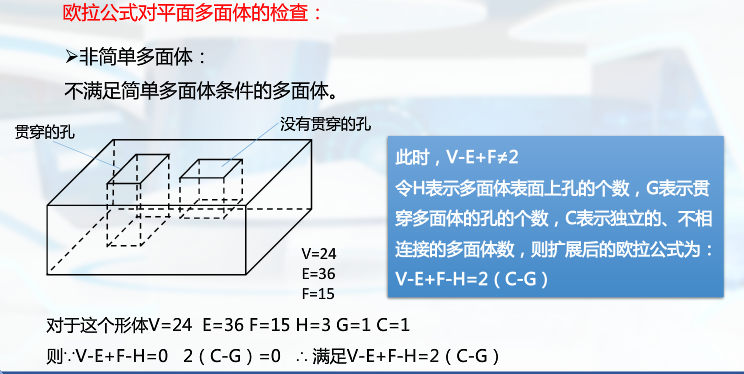
样条

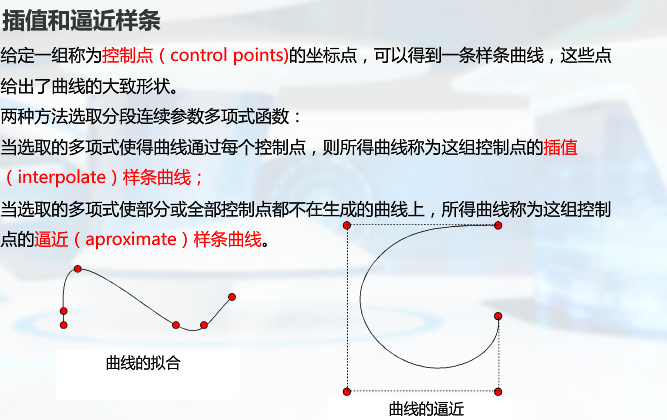
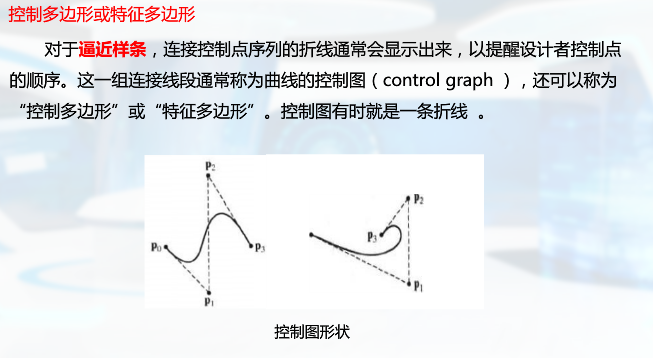

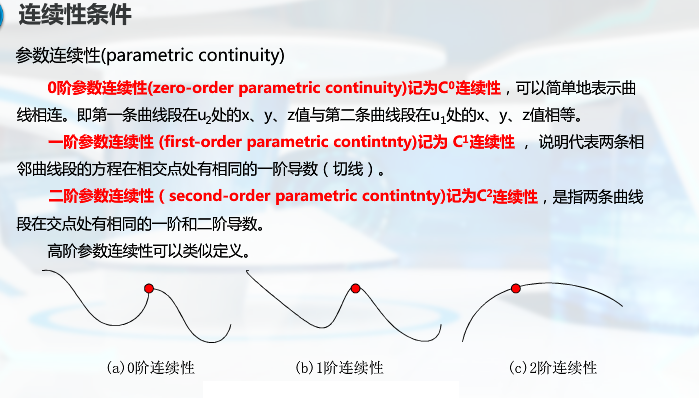

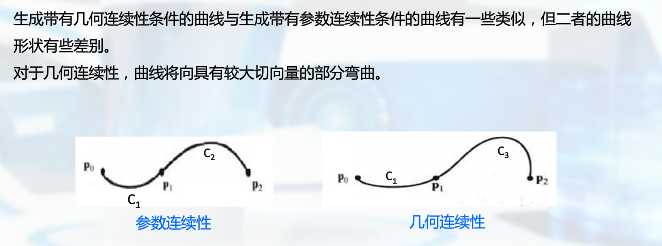
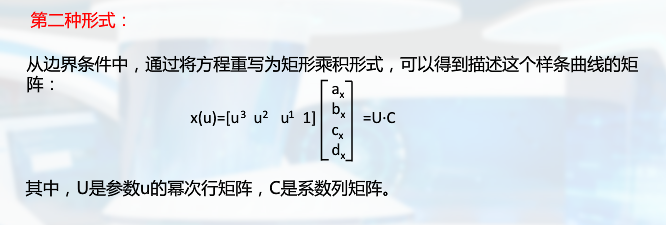
样条的描述方法





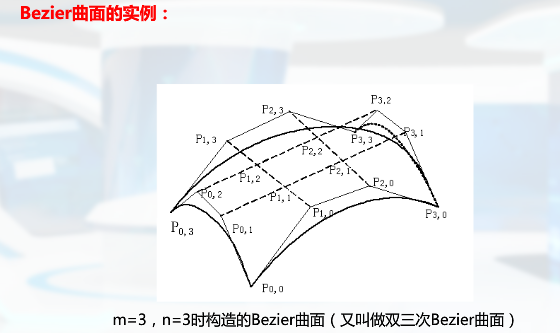
Bezier实例


特性:
(1)曲线总是通过第一个和最后一个控制点
(2)曲线起始点处的切线落在头两个控制点的连线上,曲线终点处的切线落在后两个控制点的连线上
(3)曲线落在控制点的凸壳内
(4)封闭曲线的第一个点和最后一个点重合; 多个控制点位于同一位置需要更多加权



实体模型的三类表示
多边形表示(三角形或四边形)
扫描表示(旋转扫描、广义扫描)

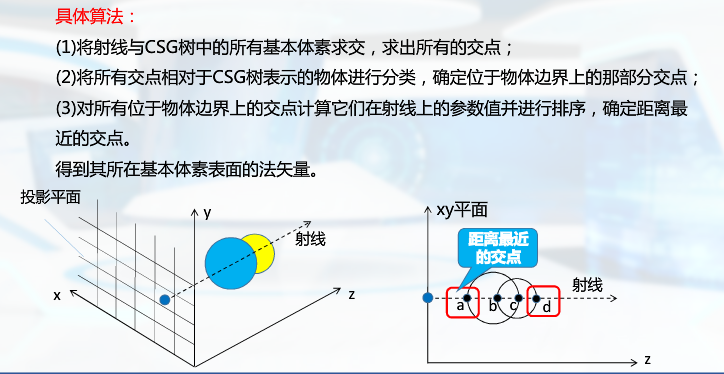
构造实体几何法:由两个实体间的并、交或差操作生成的新的实体(CSG树)

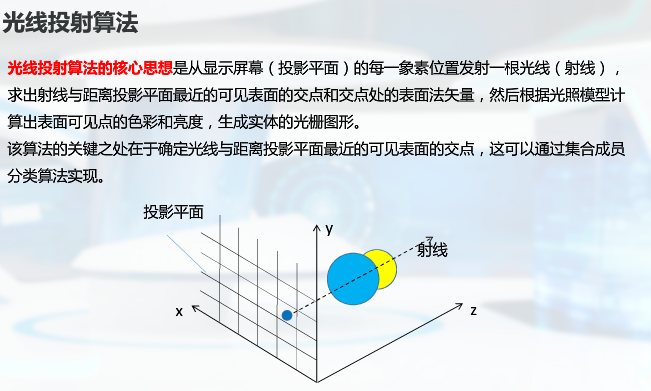
光线投射算法
空间位置枚举
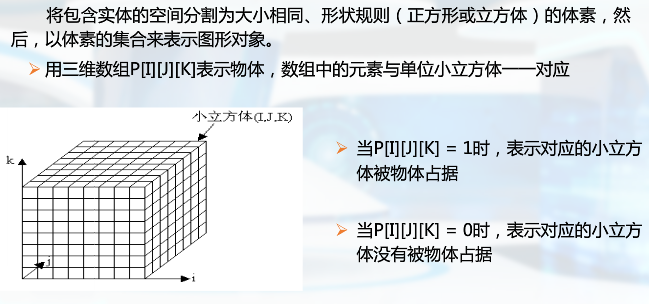
(1)八叉树
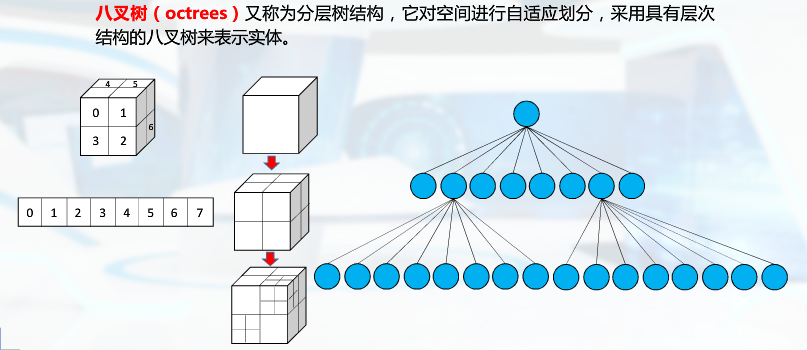
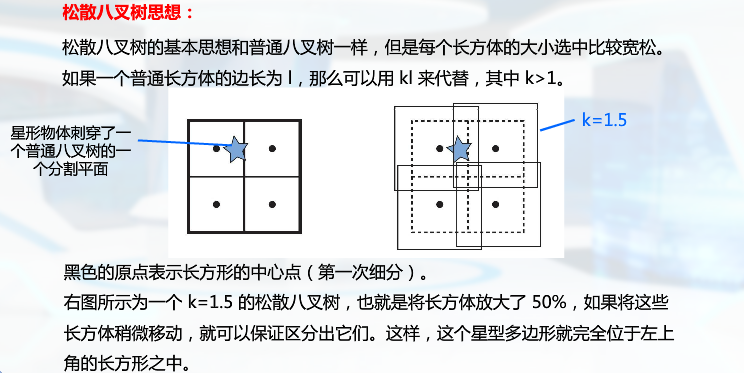
(2)松散八叉树
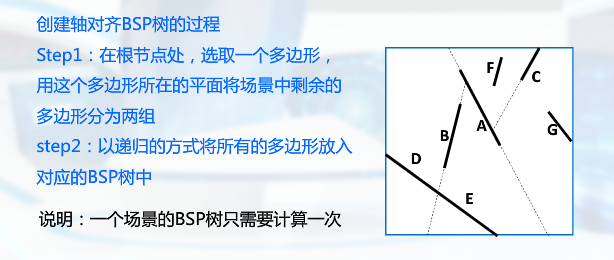
(3)BSP树
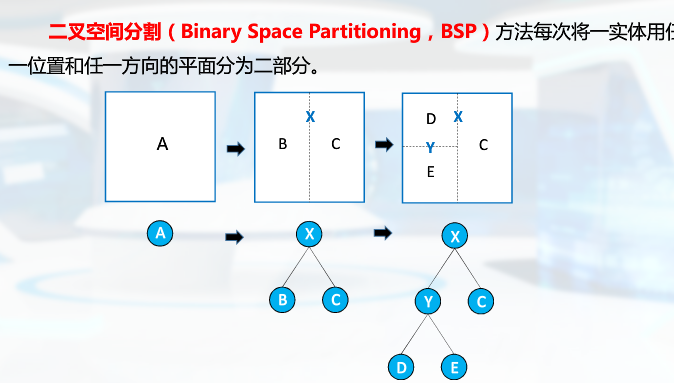
与八叉树相比较:自适应分割,有效减少树的深度和搜索时间
有效识别前向面与后向面
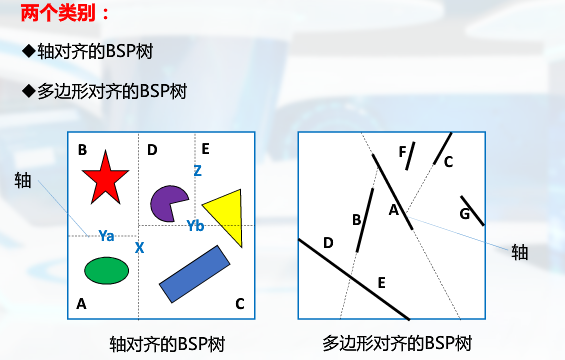
轴对齐:① xyz轴的顺序进行分割 或者 ②最长边
多边形对齐 : 常运用于深度测试、相交测试、碰撞测试
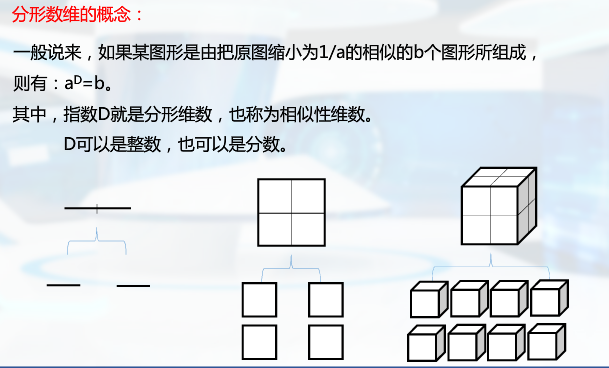
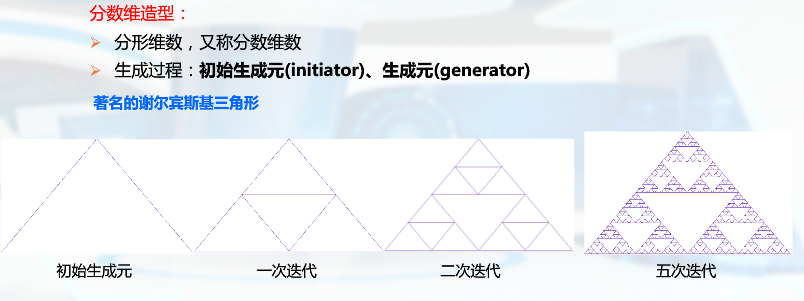
分形几何
熵:体系混乱程度的度量
分形: 具有以非整数维形式充填空间的形态特征,fractal

粒子系统
模拟火、烟、水流…

模拟多个粒子及其运动(每个粒子都有生命值)
渲染过程中粒子始终面对着摄像机方向(如NPC:Non-Player Character 的名字)

变换与观察
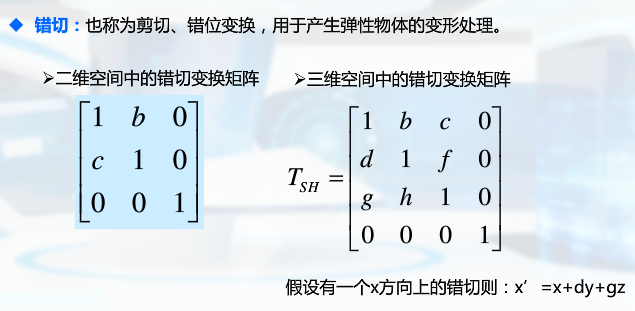
图形的几何变换是指对图形的几何信息经过平移、比例、旋转(逆时针为正方向)、对称、错切(剪切、错位变换,用于产生弹性物体的变形处理)等变换后产生新的图形
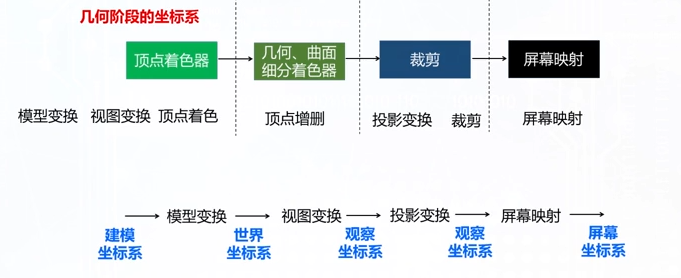
相关公式:

齐次坐标
用n+1维向量表示一个n维向量(但具有不唯一性)


运用齐次坐标可以同时表示多种变化


齐次坐标三维变换



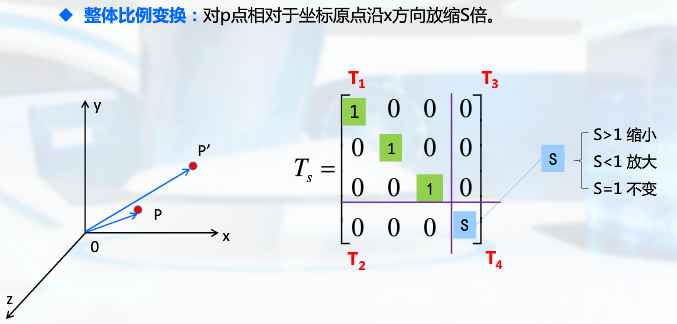
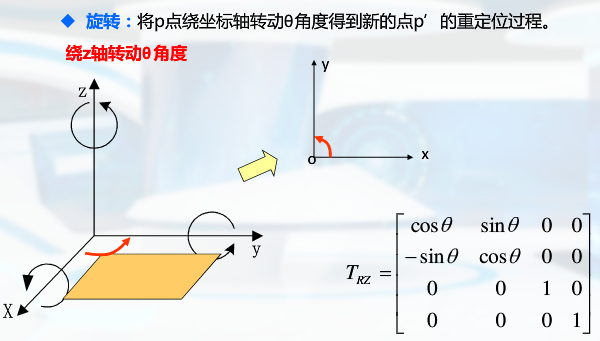
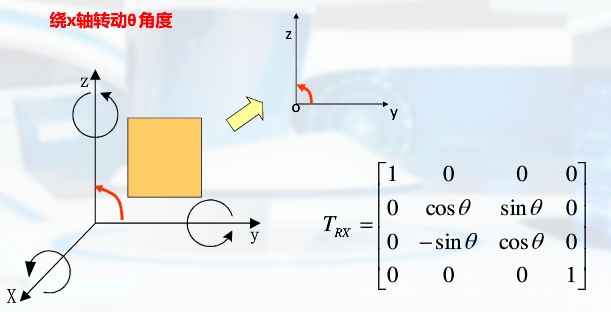
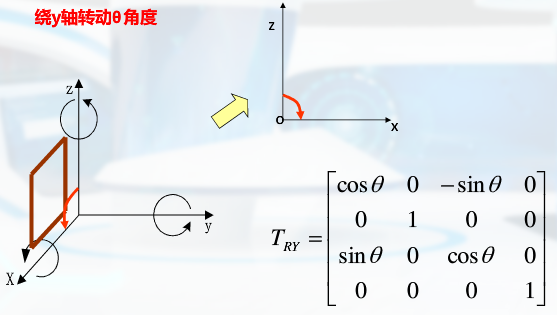
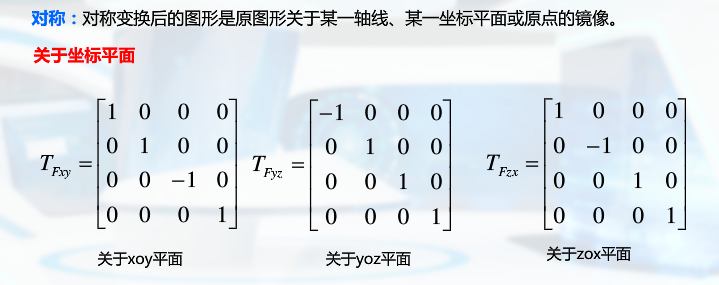
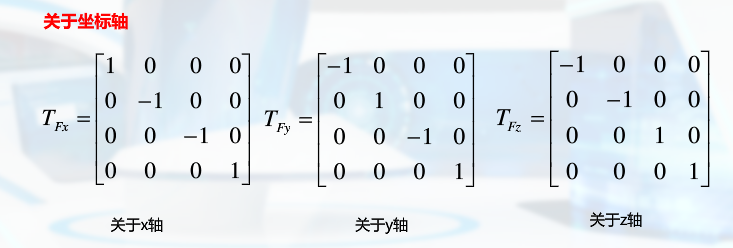
关于坐标原点:
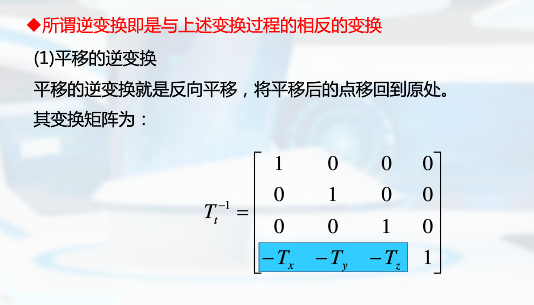
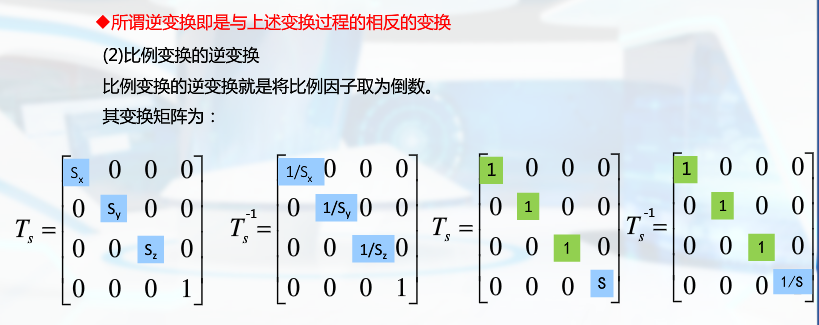

复合变化
其中三维复合变化可通过每次变换矩阵相乘来得到
(1)对任意参考点:

eg:
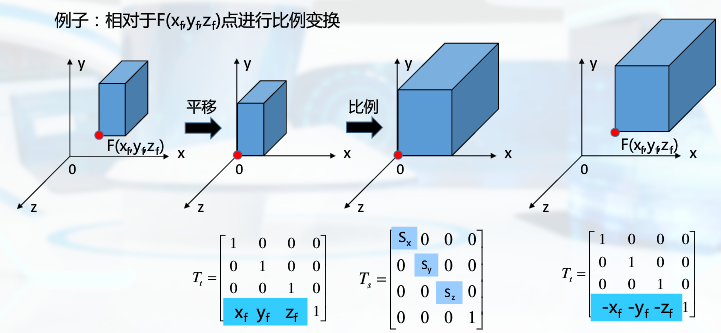
(2)对任意轴:

观察变换
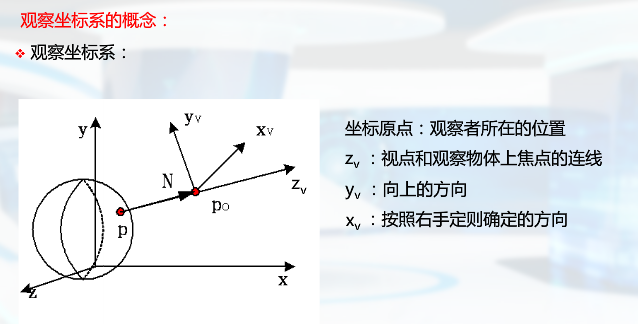
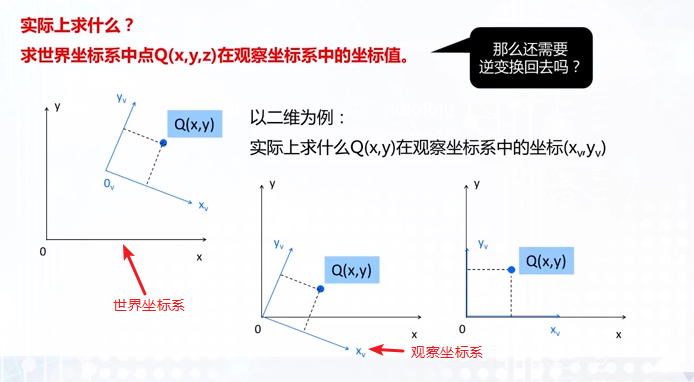
世界坐标到观察坐标系的变换 :实际上是世界坐标系Q(x,y,z)在观察坐标系中的坐标值 ,最后不需要逆变换回去
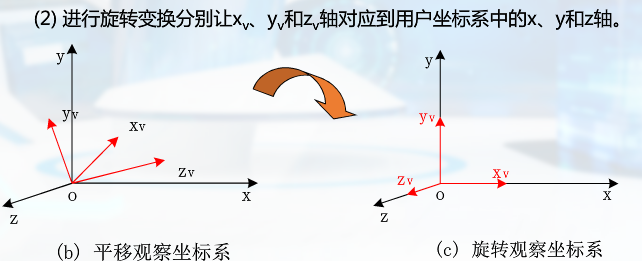
模型变化与观察变化具有对偶性
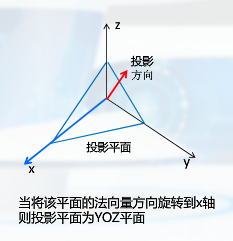
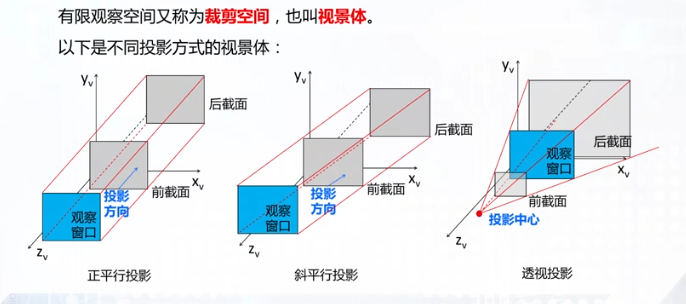
投影变换
观察变换中隐含一个观察平面,即投影平面
按照投影中心的位置
投影分类
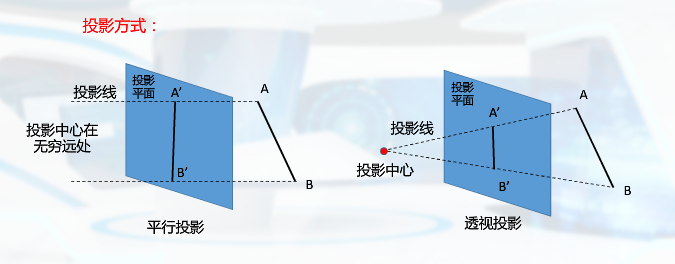
平行投影
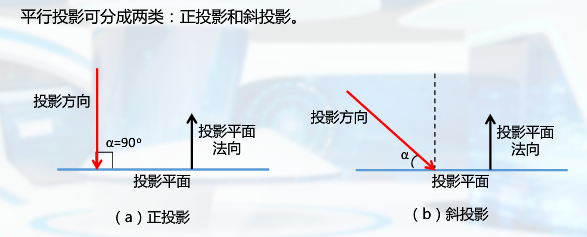
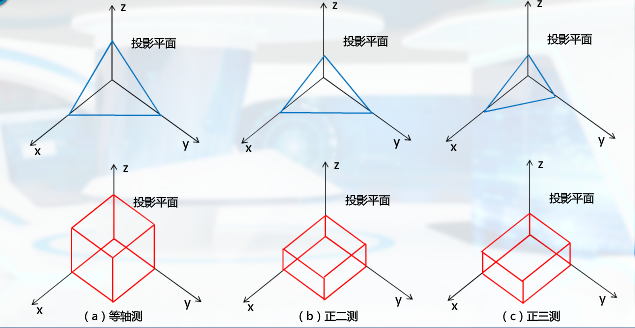
正投影分为 三视图(主侧俯)与正轴测图
等轴测:投影面与三个坐标面的夹角都相等
正二测:投影面与二个坐标面的夹角都相等
正三测:投影面与三个坐标面的夹角都不相等
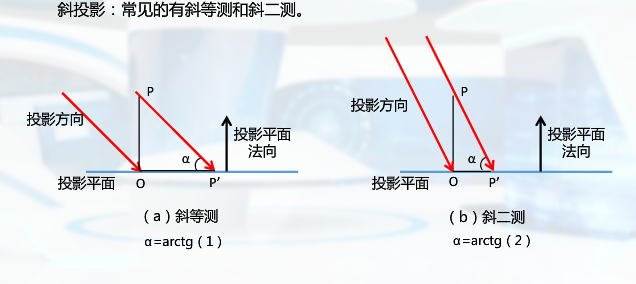
斜投影
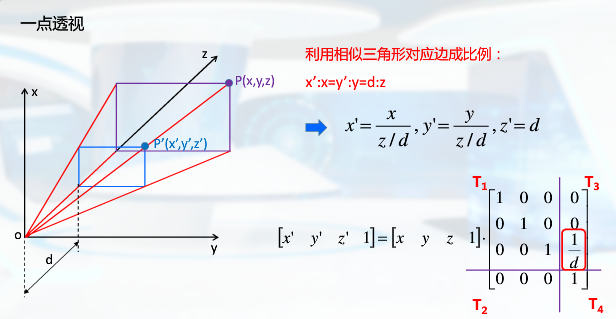
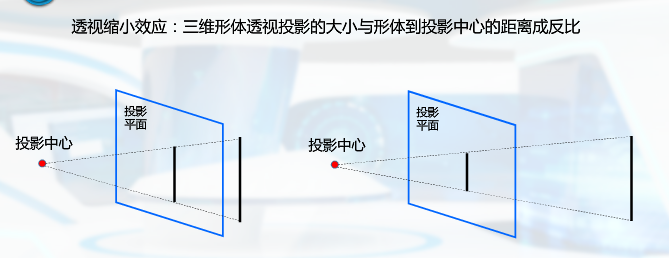
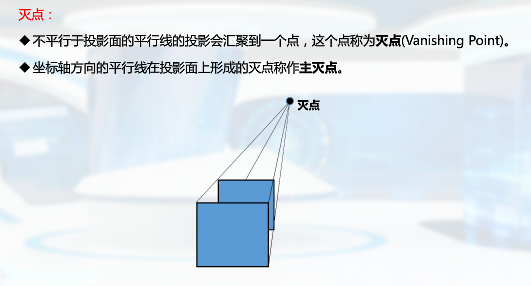
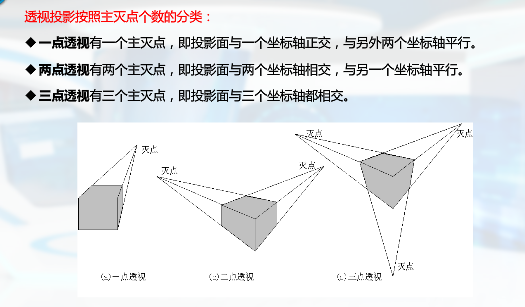
透视投影
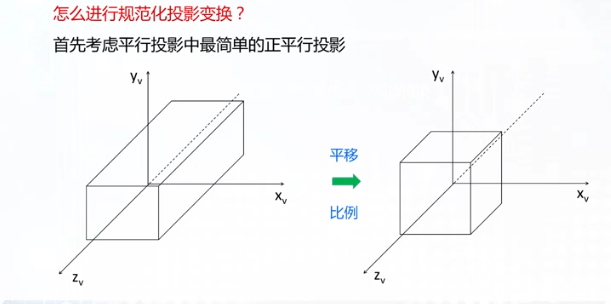
规范化投影
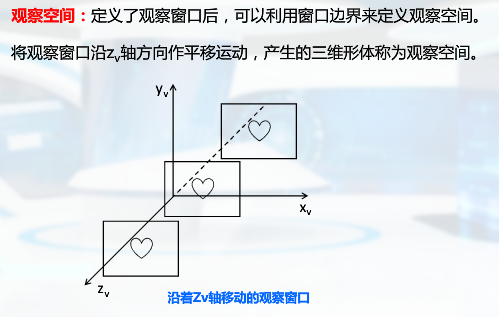
观察窗口的大小、投影方式的不同都影响着观察空间
为后续操作方便,因此规范化
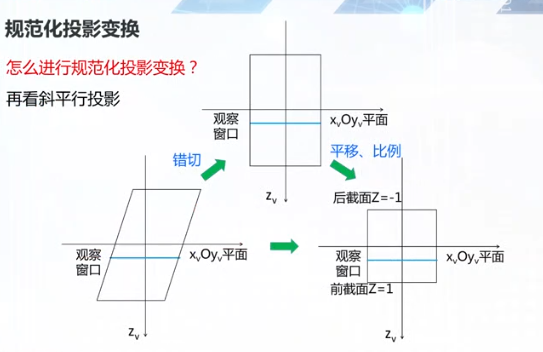
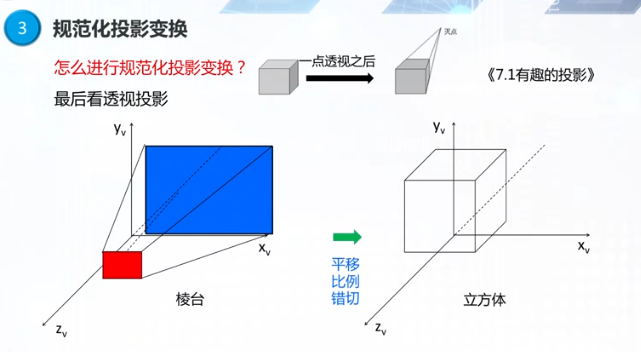
通过openGL函数调用来完成这一操作
裁剪与屏幕映射
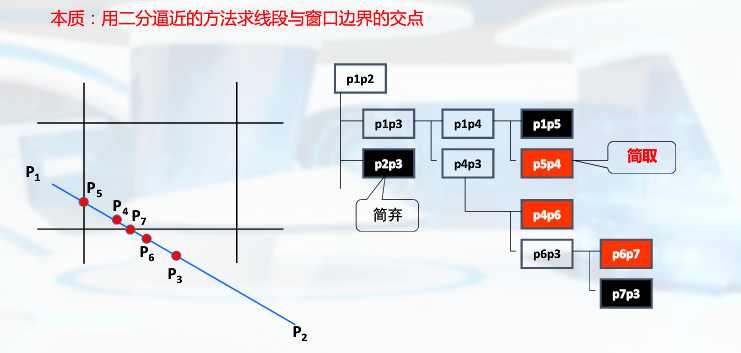
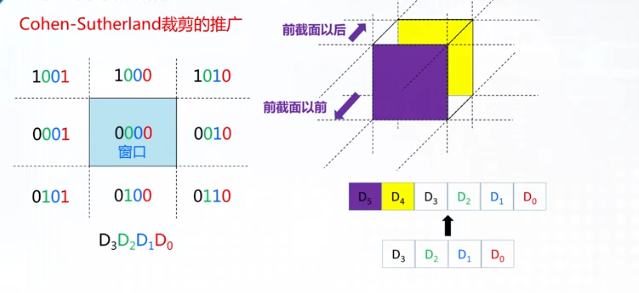
CS算法

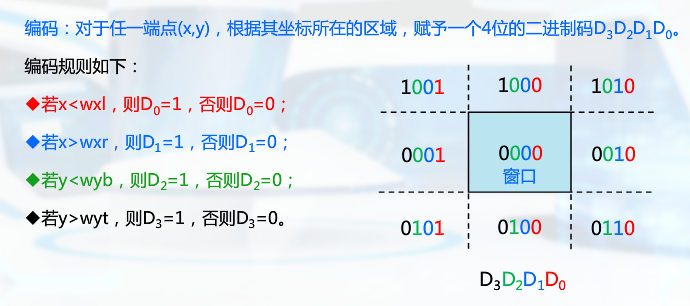
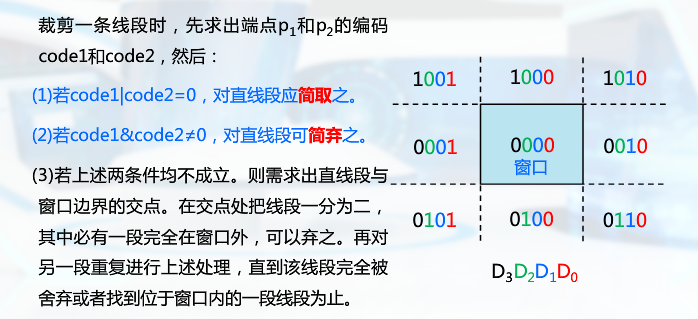
按左下右上的顺序求出直线段求出直线段与窗口边界的交点
改进后的CS中点法

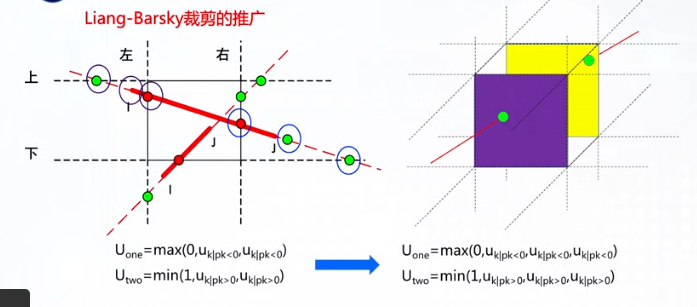
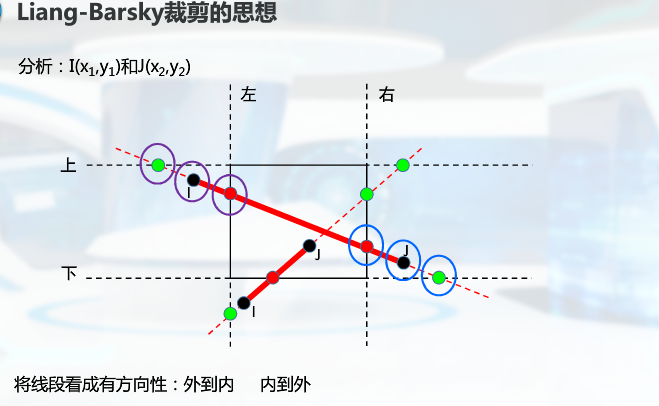
LB算法
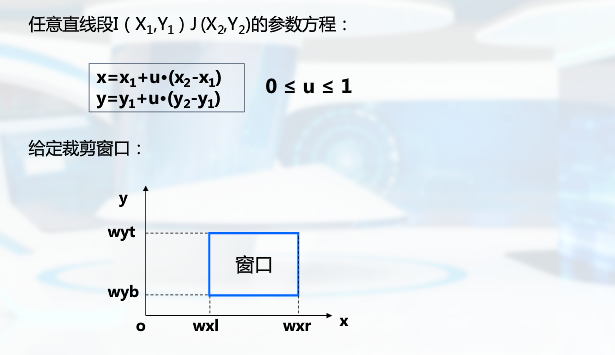
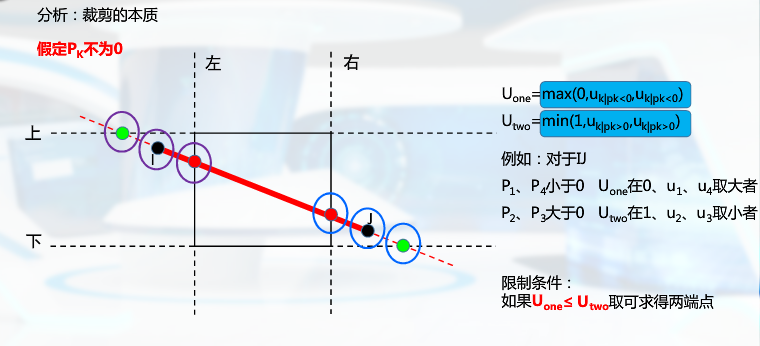
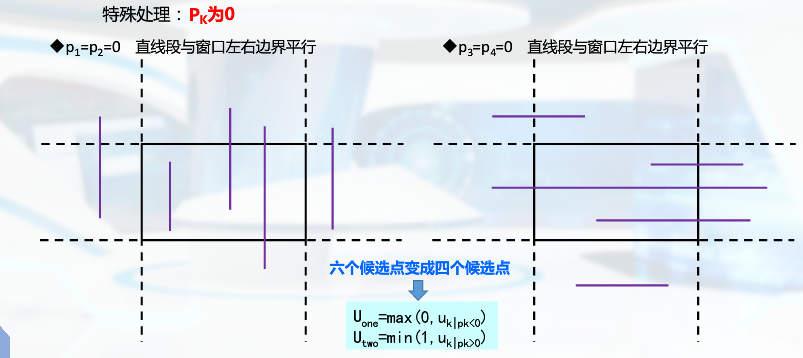
将线段看作“先进后出”的带方向的线,建立参数方程,求出与裁剪窗口的交点,6个点:起终点,与窗口边界及其延长线的交点


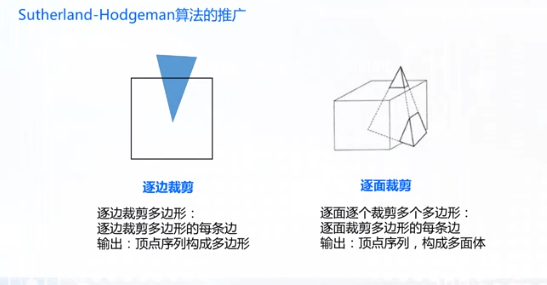
多边形的裁剪
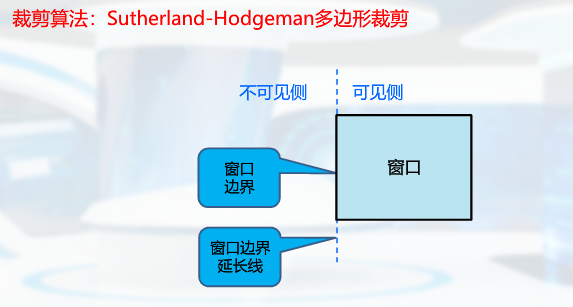
该算法遇到凹边形时会出现问题:多余边V2、V3
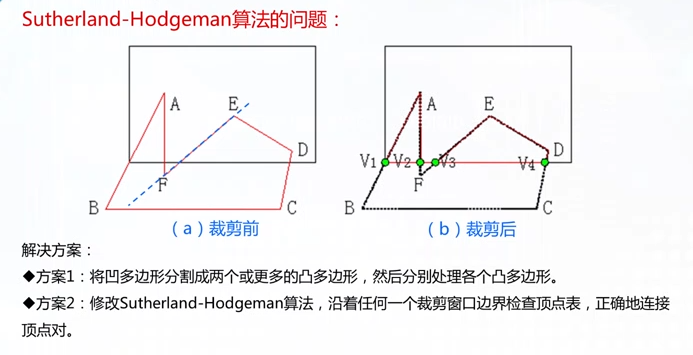
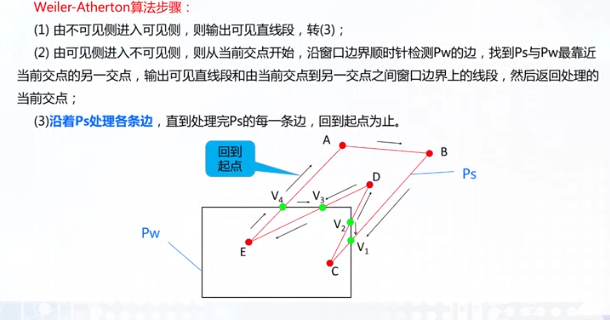
另一种算法
窗口定义为pw,多边形定义为ps
线段按指定方向,在可见侧进入不可见侧时进行相应操作(以BC,CD为例 到V2时同时输出V1、V2,并返回D点)
三维空间的裁剪
增加至6个点,与面的交点
增加至8个点,与面的交点