基本概念
在“无监督学习” 任务中研究最多、 应用最广。
聚类目标:将数据集中的样本划分为若干个通常不相交的子集(“簇” , cluster)
聚类既可以作为一个单独过程(用于找寻数据内在的分布结构) , 也可作为分类等其他学习任务的前驱过程。
应用:1,分析数据内在结构;2,作为有监督学习的预处理部分,发掘数据的隐藏模式
| 监督信号类别 | ||||
|---|---|---|---|---|
| 任务标注 | 中间激励 | 无 | ||
| 输出 | 离散 | 分类 | 聚类 | |
| 连续 | 回归 | 降维 | ||
| 策略 | 模仿学习 | 强化学习 |
聚类性能指标(聚类结果的“簇内相似度”(intra-cluster similarity) 高,且“簇间相似度”(inter-cluster
similarity)低 )
外部指标:将聚类结果与某个“参考模型”(只用于测试评判) 进行比较
内部指标(划分依据):基于簇内和簇间相似度直接考察聚类结果
a=SS (一致)、b=SD(不一致) c=DS、d=DD(若一致)
外部指标 ([0,1]区间内,越大越好 )
Jaccard系数(Jaccard Coefficient, JC)
FM指数(Fowlkes and Mallows Index, FMI)
Rand指数(Rand Index, RI)
内部指标
考虑聚类结果的簇C划分 ,定义:簇 C内样本间的平均距离(簇内距离) 、簇 C 内样本间的最远距离(簇内距离)、簇C_i与簇 C_j最近样本间的距离(簇间距离)、簇 C_i与簇 C_j中心点间的距离(簇间距离)
DB指数(Davies-Bouldin Index, DBI) (簇内距离)
Dunn指数(Dunn Index, DI) (簇间距离)
距离度量
性质:非负性、同一性、对称性、直递性
闵可夫斯基距离(Minkowski distance)
p=2: 欧氏距离(Euclidean distance).
p=1: 曼哈顿距离(Manhattan distance)
分类
基于原型的聚类(Prototype-based clustering)
• 主要特点:先对原型进行初始化,然后进行迭代更新
• 常见算法: k-Means算法,高斯混合模型
基于密度的聚类(Density-based clustering)
• 主要特点:从样本密度的角度来考察样本间的关系
• 常见算法: DBSCAN算法
层次聚类(Hierarchical clustering)
• 主要特点:在不同层次对样本进行划分,形成树形的聚类结构
• 常见算法: 逐次聚合算法
k-Means算法
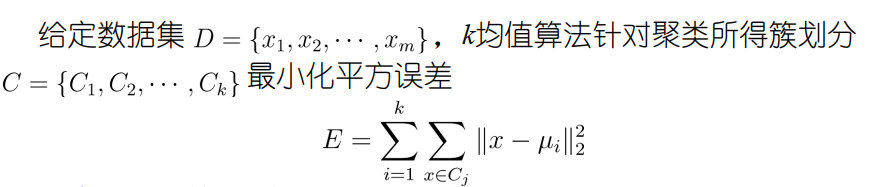
E值在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度,
值越小,则簇内样本相似度越高。
算法流程(迭代优化):
人工选取簇的个数,初始化每个簇的均值向量(中心)
repeat
- 簇划分(聚类);
- 更新每个簇的中心
until 当前均值向量均未更新
不足:
簇的数目k需要人为指定;对簇中心的初始化比较敏感;破坏数据内在结构
ps:
硬聚类:样本只从属于一个簇,如K-means
软聚类:样本以该概率从属于多个簇,如高斯混合模型、EM模型
混合模型是概率化的k-Means算法
基于密度的聚类
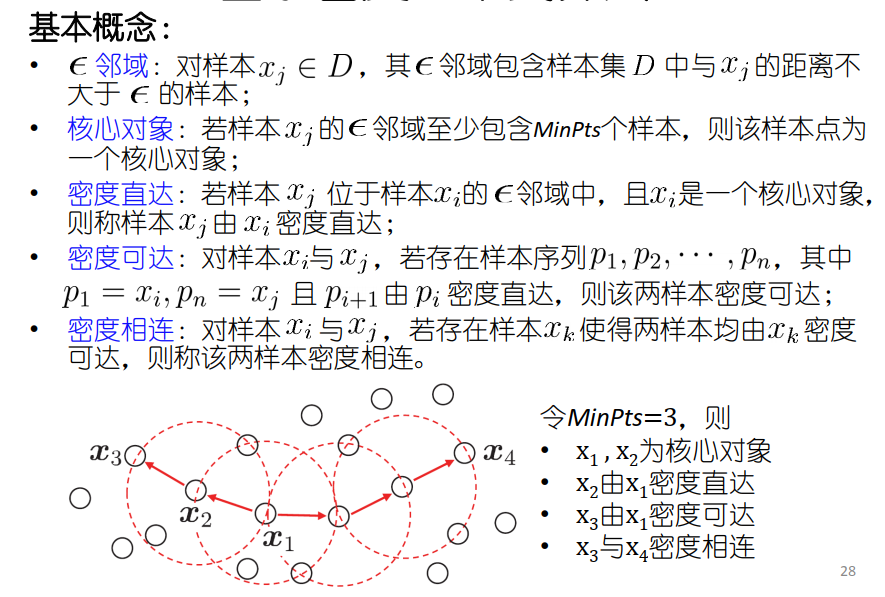
DBSCAN算法(举例)
簇的定义:密度相连样本组成的集
算法的核心:由核心对象搜寻密度可达的所有样本

Agglomerative(逐次聚合)算法
算法过程(自底向上的层次聚类):
• 首先,将样本中的每一个样本看做一个初始聚类簇;
• 然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,
该过程不断重复,直到达到预设的聚类簇的个数。
• 基于层次的聚类
• 生成不同层次的簇-树状图