互相关运算和卷积运算
实际上,卷积运算与互相关运算类似。为了得到卷积运算的输出,我们只需将核数组左右翻转并上下翻转,再与输入数组做互相关运算。可见,卷积运算和互相关运算虽然类似,但如果它们使用相同的核数组,对于同一个输入,输出往往并不相同。
那么,你也许会好奇卷积层为何能使用互相关运算替代卷积运算。其实,在深度学习中核数组都是学出来的:卷积层无论使用互相关运算或卷积运算都不影响模型预测时的输出。
二维卷积层的核心计算是二维互相关运算。在最简单的形式下,它对二维输入数据和卷积核做互相关运算然后加上偏差。
特征图和感受野
二维卷积层输出的二维数组可以看作是输入在空间维度(宽和高)上某一级的表征,也叫特征图(feature map)。影响元素x的前向计算的所有可能输入区域(可能大于输入的实际尺寸)叫做x的感受野(receptive field)。
以图为例,输入中阴影部分的四个元素是输出中阴影部分元素的感受野。我们将图中形状为2×2的输出记为Y,并考虑一个更深的卷积神经网络:将Y与另一个形状为2×2的核数组做互相关运算,输出单个元素z。那么,z在Y上的感受野包括Y的全部四个元素,在输入上的感受野包括其中全部9个元素。可见,我们可以通过更深的卷积神经网络使特征图中单个元素的感受野变得更加广阔,从而捕捉输入上更大尺寸的特征。
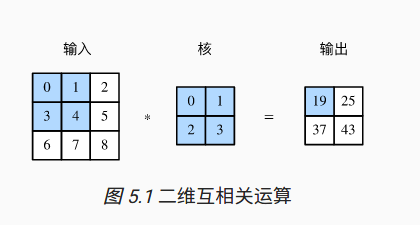
我们常使用“元素”一词来描述数组或矩阵中的成员。在神经网络的术语中,这些元素也可称为“单元”。
一般来说,假设输入形状是nh×nw,卷积核窗口形状是kh×kw,那么输出形状将会是(nh−kh+1)×(nw−kw+1).
所以卷积层的输出形状由输入形状和卷积核窗口形状决定。本节我们将介绍卷积层的两个超参数,即填充和步幅。它们可以对给定形状的输入和卷积核改变输出形状。
padding
为防止卷积将图片变小,损失信息,在此操作前先进行填充。
一般来说,如果在高的两侧一共填充ph行,在宽的两侧一共填充pw
列,那么输出形状将会是(nh−kh+ph+1)×(nw−kw+pw+1),
也就是说,输出的高和宽会分别增加ph和pw
在很多情况下,我们会设置ph=kh−1和pw=kw−1来使输入和输出具有相同的高和宽。这样会方便在构造网络时推测每个层的输出形状。假设这里kh是奇数,我们会在高的两侧分别填充ph/2行。如果kh是偶数,一种可能是在输入的顶端一侧填充⌈ph/2⌉行,而在底端一侧填充⌊ph/2⌋行。在宽的两侧填充同理。
卷积神经网络经常使用奇数高宽的卷积核,如1、3、5和7,所以两端上的填充个数相等。对任意的二维数组X,设它的第i行第j列的元素为X[i,j]。当两端上的填充个数相等,并使输入和输出具有相同的高和宽时,我们就知道输出Y[i,j]是由输入以X[i,j]为中心的窗口同卷积核进行互相关计算得到的

卷积步长
一般来说,当高上步幅为sh,宽上步幅为sw时,输出形状为
⌊(nh−kh+ph+sh)/sh⌋×⌊(nw−kw+pw+sw)/sw⌋.
如果设置ph=kh−1和pw=kw−1,那么输出形状将简化为⌊(nh+sh−1)/sh⌋×⌊(nw+sw−1)/sw⌋。更进一步,如果输入的高和宽能分别被高和宽上的步幅整除,那么输出形状将是(nh/sh)×(nw/sw)。
过滤器必须处于图像中或者填充之后得图像区域内,采用向下取整的方法。

在机器学习领域一般没有翻转操作,也叫卷积,但是实际上是互相关操作(cross-correlation)。
多通道输入
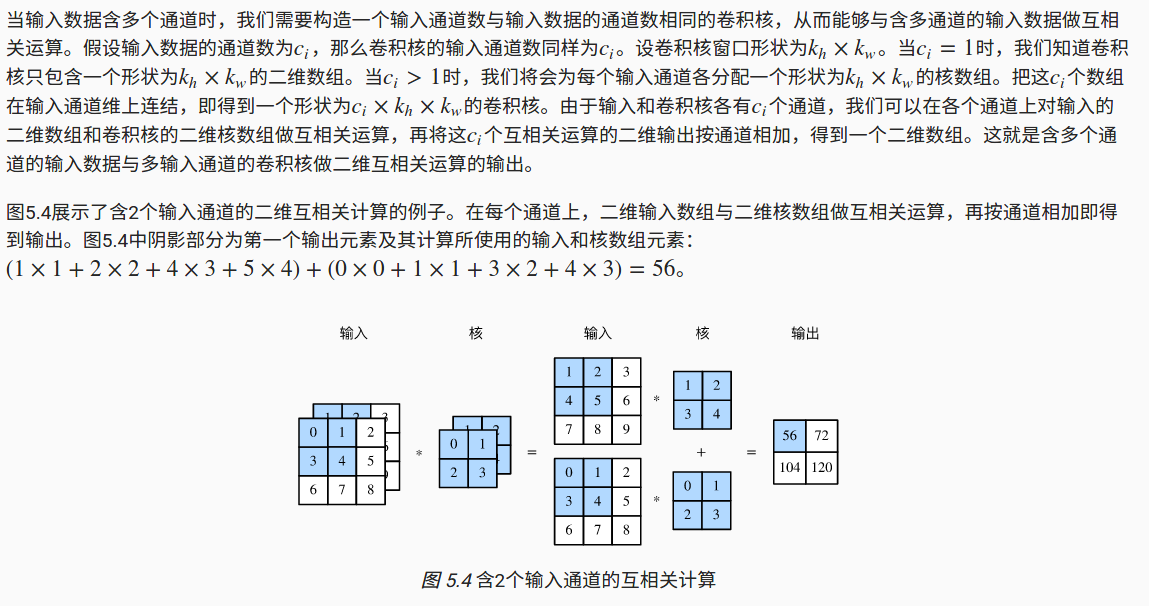
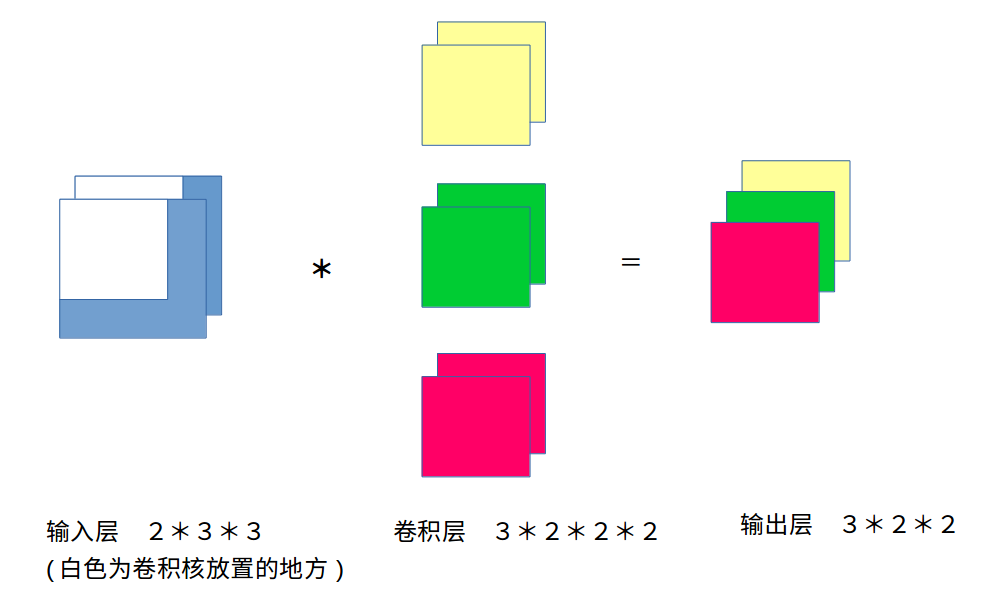
多通道输出

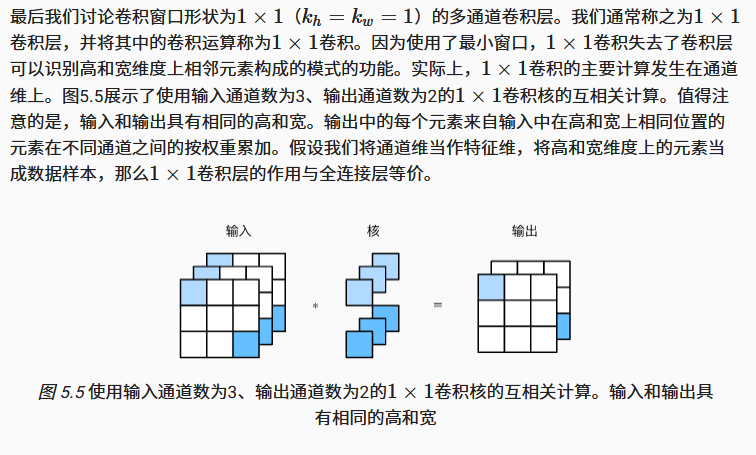
1*1卷积层
1×1卷积层被当作保持高和宽维度形状不变的全连接层使用。于是,我们可以通过调整网络层之间的通道数来控制模型复杂度。
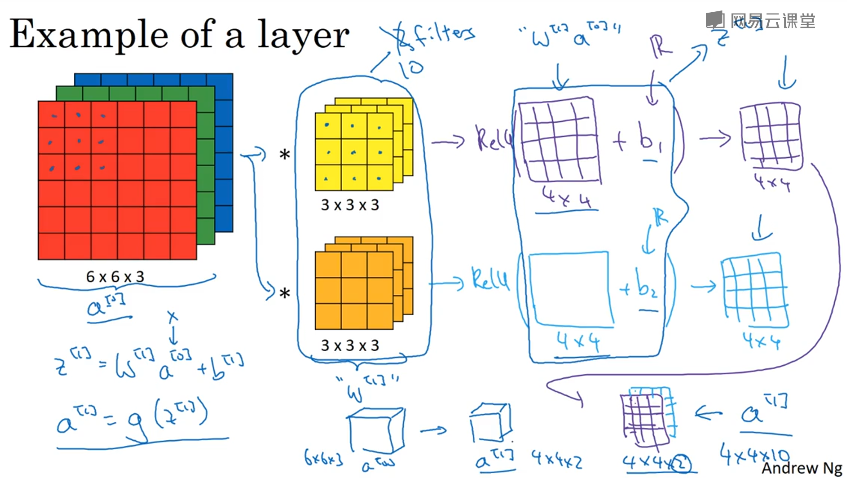
单层卷积网络
特征 “防止过拟合”


一般卷积神经网络的结构:

全连接层
输出层中的神经元和输入层中各个输入完全连接(即:输入和输出全连接)。因此,这里的输出层又叫全连接层(fully-connected layer)或稠密层(dense layer)。梯度会指向各点处的函数值降低的方向。更严格的讲,梯度指示的方向是各点处的函数值减少最多的方向。(采用梯度下降法)
全连接层:上一层与该层(full connect)的每个单元相连接
池化层(pooling)
它的提出是为了缓解卷积层对位置的过度敏感性。
举例:实际图像里,我们感兴趣的物体不会总出现在固定位置:即使我们连续拍摄同一个物体也极有可能出现像素位置上的偏移。这会导致同一个边缘对应的输出可能出现在卷积输出Y中的不同位置,进而对后面的模式识别造成不便。
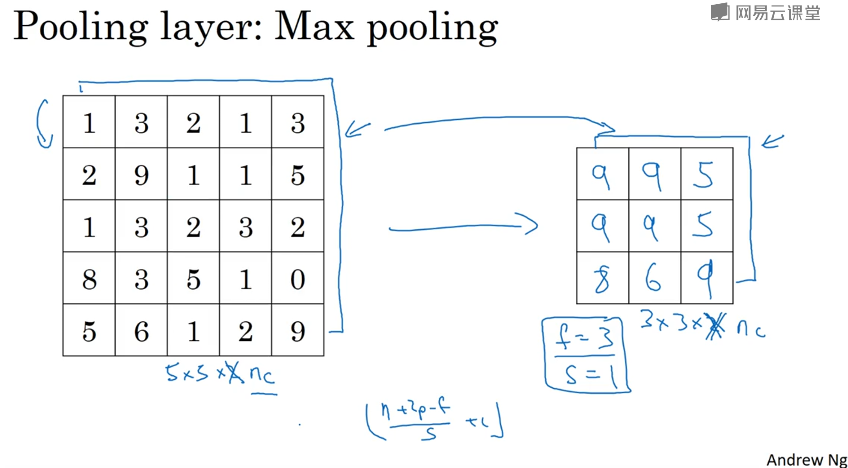
池化层每次对输入数据的一个固定形状窗口(又称池化窗口)中的元素计算输出。不同于卷积层里计算输入和核的互相关性,池化层直接计算池化窗口内元素的最大值或者平均值。该运算也分别叫做最大池化或平均池化。
池化层的输出通道数跟输入通道数相同。
因为在处理多通道输入数据时,池化层对每个输入通道分别池化,而不是像卷积层那样将各通道的输入按通道相加。
作用:最大池化层,增强图片亮度;平均池化层,减少冲击失真,模糊,平滑。
最大池化层(常用)
平均池化层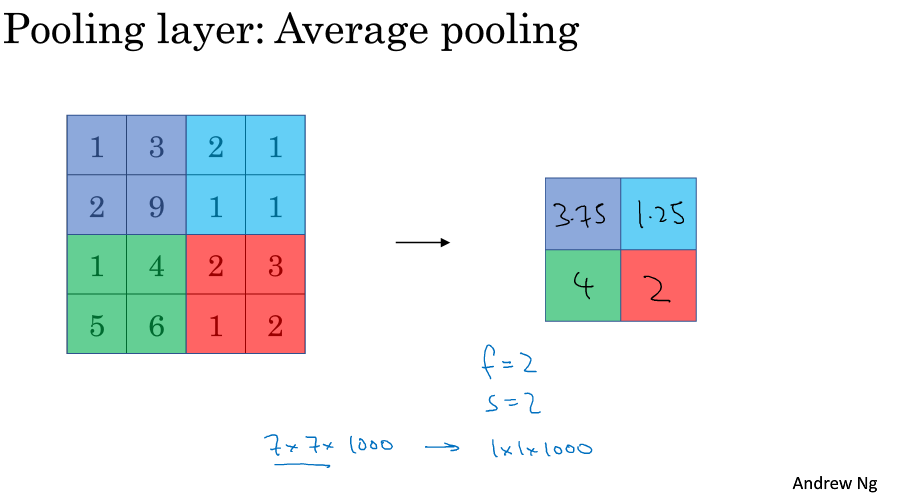
小结
- 填充可以增加输出的高和宽。这常用来使输出与输入具有相同的高和宽。
- 步幅可以减小输出的高和宽,例如输出的高和宽仅为输入的高和宽的1/n(n为大于1的整数)。
- 最大池化和平均池化分别取池化窗口中输入元素的最大值和平均值作为输出。
- 池化层的一个主要作用是缓解卷积层对位置的过度敏感性。
- 可以指定池化层的填充和步幅。
- 池化层的输出通道数跟输入通道数相同。
CNN
卷积神经网络就是含卷积层的网络
卷积层尝试解决这两个问题。一方面,卷积层保留输入形状,使图像的像素在高和宽两个方向上的相关性均可能被有效识别;另一方面,卷积层通过滑动窗口将同一卷积核与不同位置的输入重复计算,从而避免参数尺寸过大。
计算神经网络有多少层时,通常只统计具有权重和参数的层。有时将卷积层和池化层计为1层
卷积神经网络的优点:参数共享和稀疏连接来减少参数,用于训练更小的训练集以及防止过拟合。
CNN举例
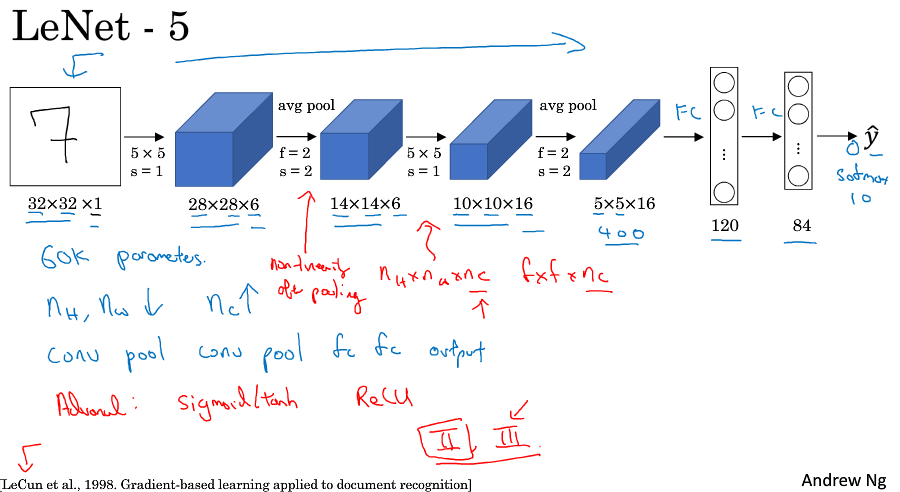
LeNet模型
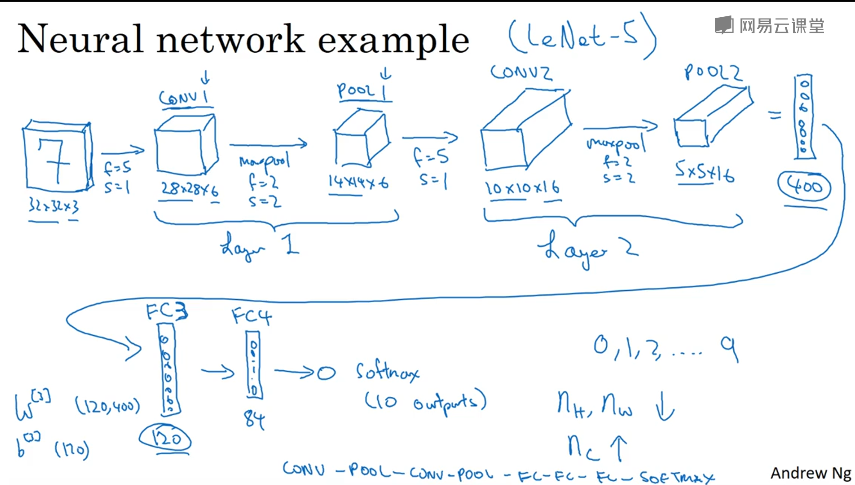
分为卷积层块和全连接层块两个部分
卷积层块里的基本单位是卷积层后接最大池化层:卷积层用来识别图像里的空间模式,如线条和物体局部,之后的最大池化层则用来降低卷积层对位置的敏感性。卷积层块由两个这样的基本单位重复堆叠构成。在卷积层块中,每个卷积层都使用5×5的窗口,并在输出上使用sigmoid激活函数。第一个卷积层输出通道数为6,第二个卷积层输出通道数则增加到16。这是因为第二个卷积层比第一个卷积层的输入的高和宽要小,所以增加输出通道使两个卷积层的参数尺寸类似。卷积层块的两个最大池化层的窗口形状均为2×2,且步幅为2。由于池化窗口与步幅形状相同,池化窗口在输入上每次滑动所覆盖的区域互不重叠。
卷积层块的输出形状为(批量大小, 通道, 高, 宽)。当卷积层块的输出传入全连接层块时,全连接层块会将小批量中每个样本变平(flatten)。也就是说,全连接层的输入形状将变成二维,其中第一维是小批量中的样本,第二维是每个样本变平后的向量表示,且向量长度为通道、高和宽的乘积。全连接层块含3个全连接层。它们的输出个数分别是120、84和10,其中10为输出的类别个数。
其他传统网络
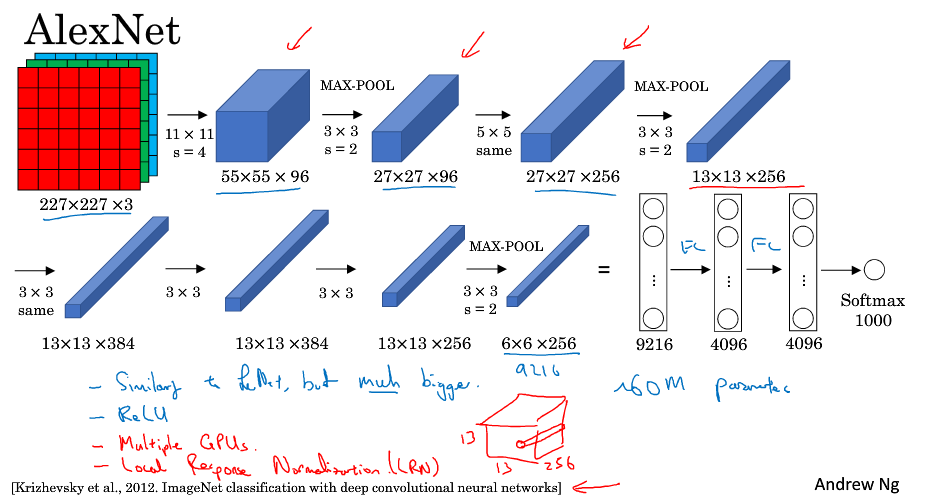
AlexNet
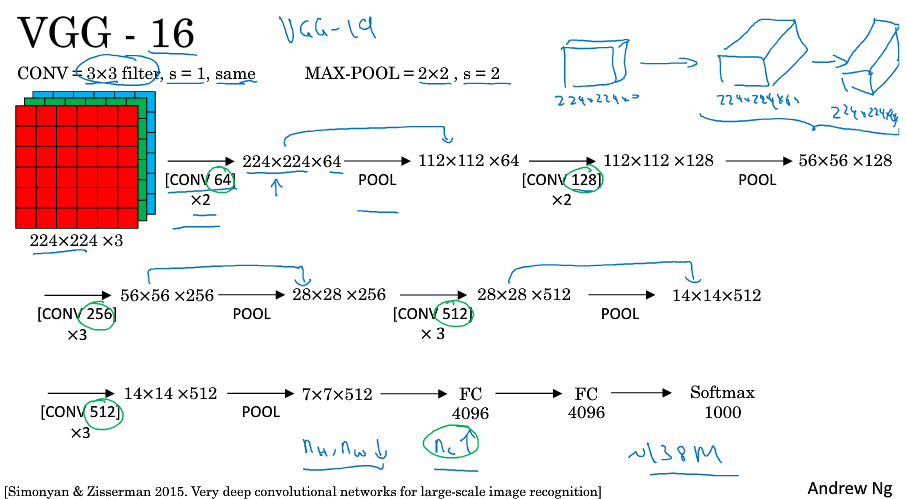
VGG16
残差网络
有助于解决梯度消失和梯度爆炸问题,也能保证深层网络良好的性能
跳远连接:a^[l]数据传送到更远的层
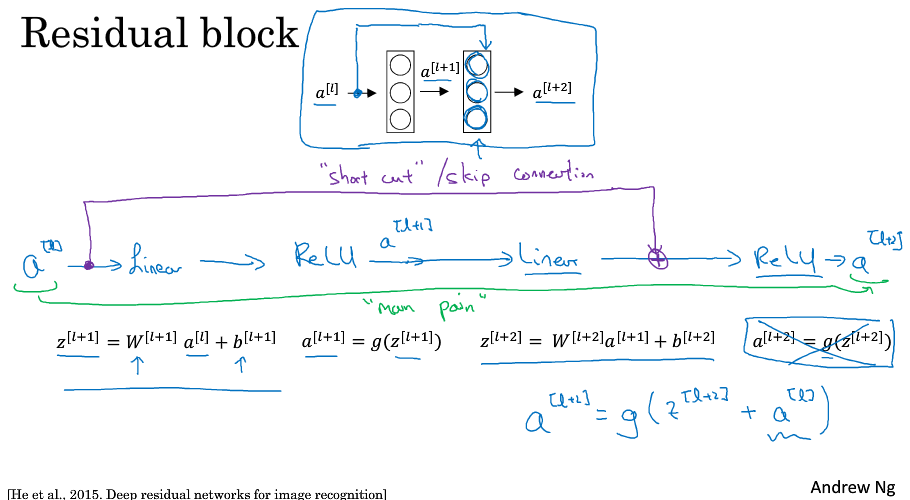
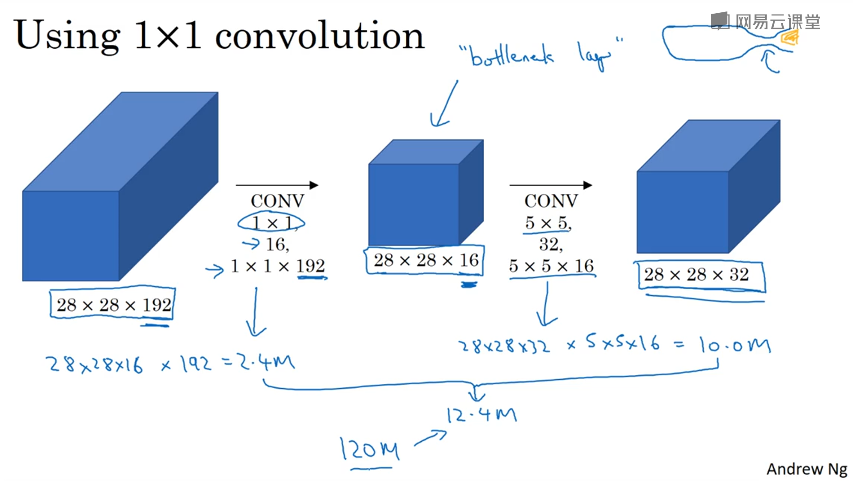
通过1*1卷积来压缩或保持输入层中信道数量
Inception网络
不需要人为决定使用那个过滤器或是否需要池化,通过合理构建瓶颈层,可以缩小表示层规模,而又不降低网络性能。
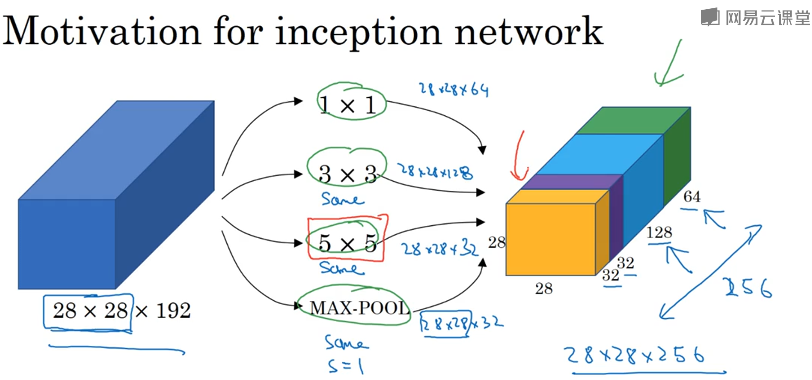
但是直接这样做计算成本太高。
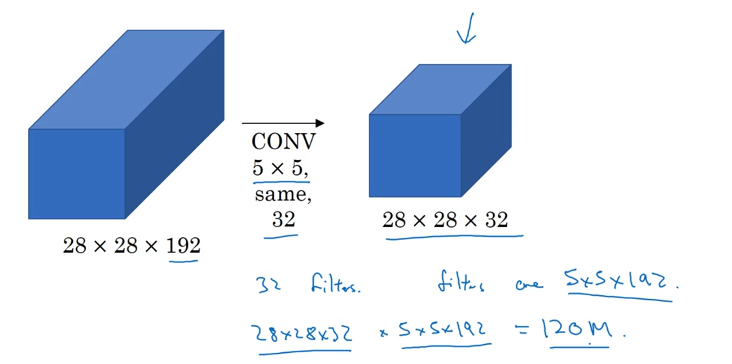
利用1*1卷积层做瓶颈层