机器学习-评价方法

模型选择

60% 训练集 20%验证集 20%测试集

训练集计算误差，利用交叉验证集选择维数，泛化能力

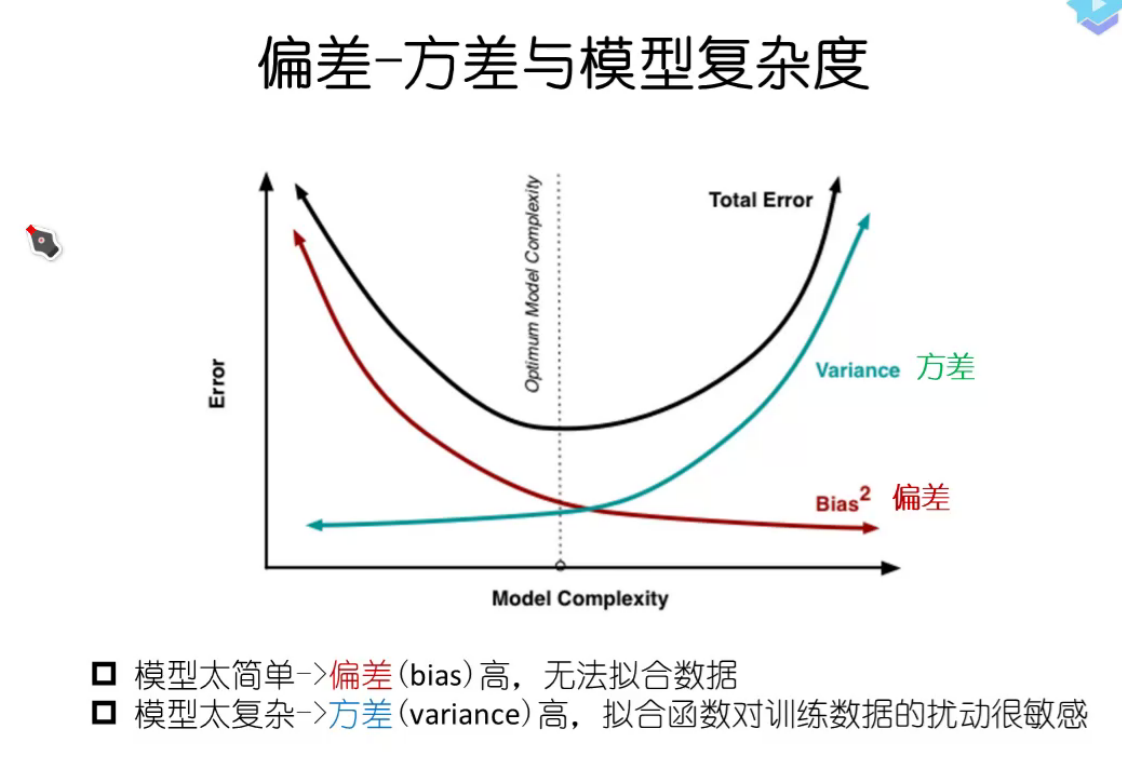
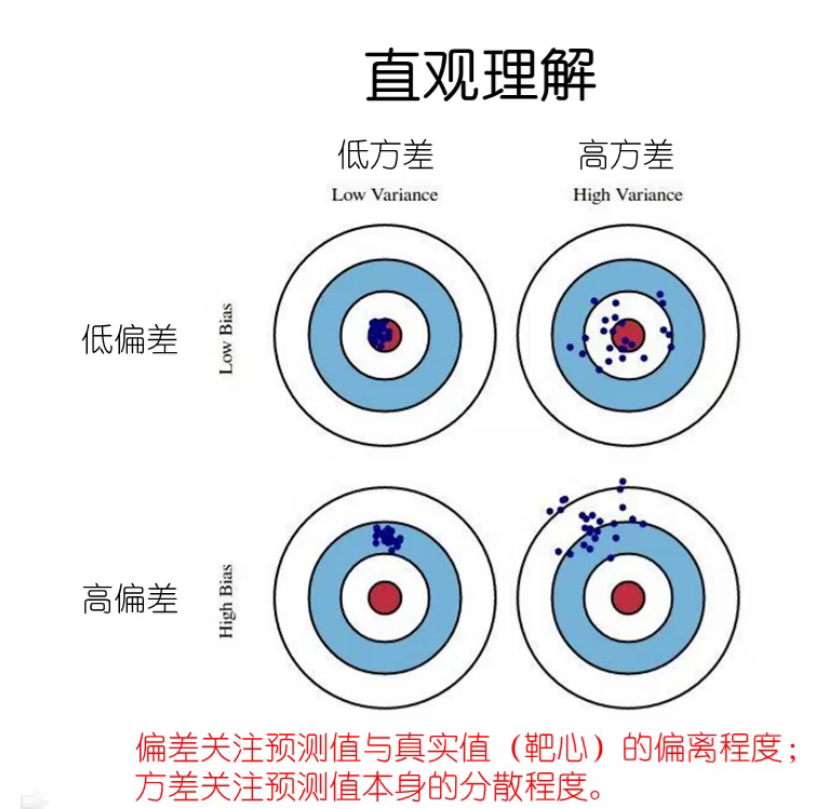
偏差与方差

偏差（与训练集数据拟合程度），方差（与验证集数据拟合程度）

项数少 ：高偏差，高方差

项数多：低偏差，高方差

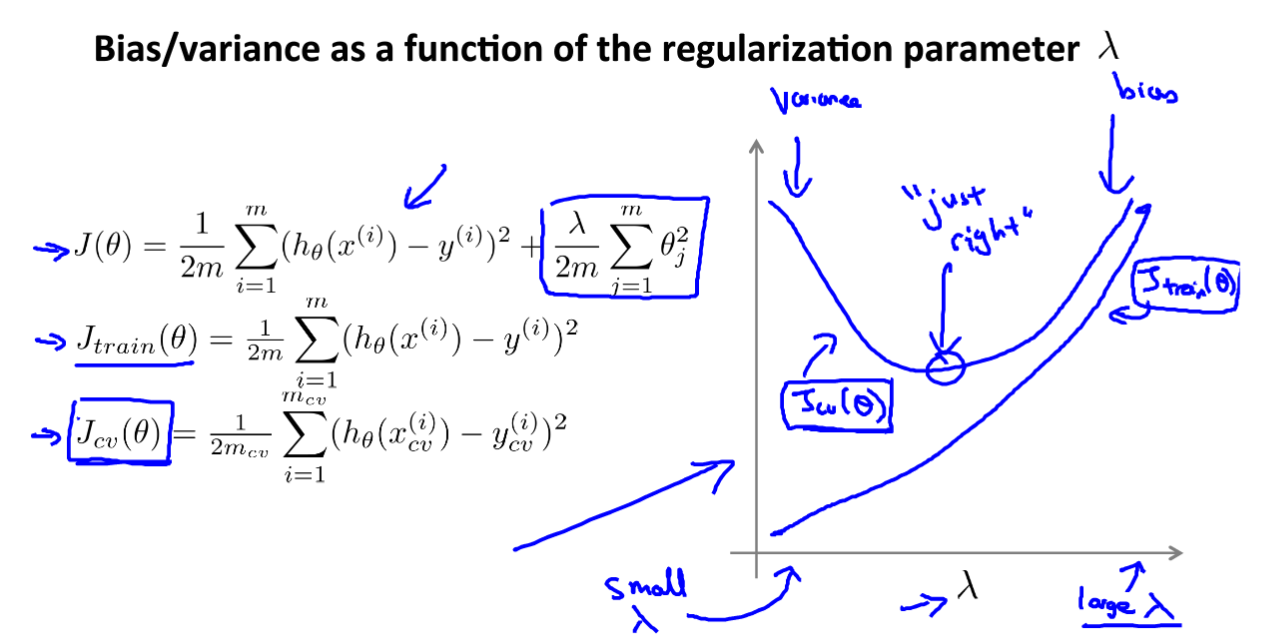
正则化：防止过拟合

lambda 小 ：低偏差，高方差

lambda大：高偏差，高方差

学习曲线

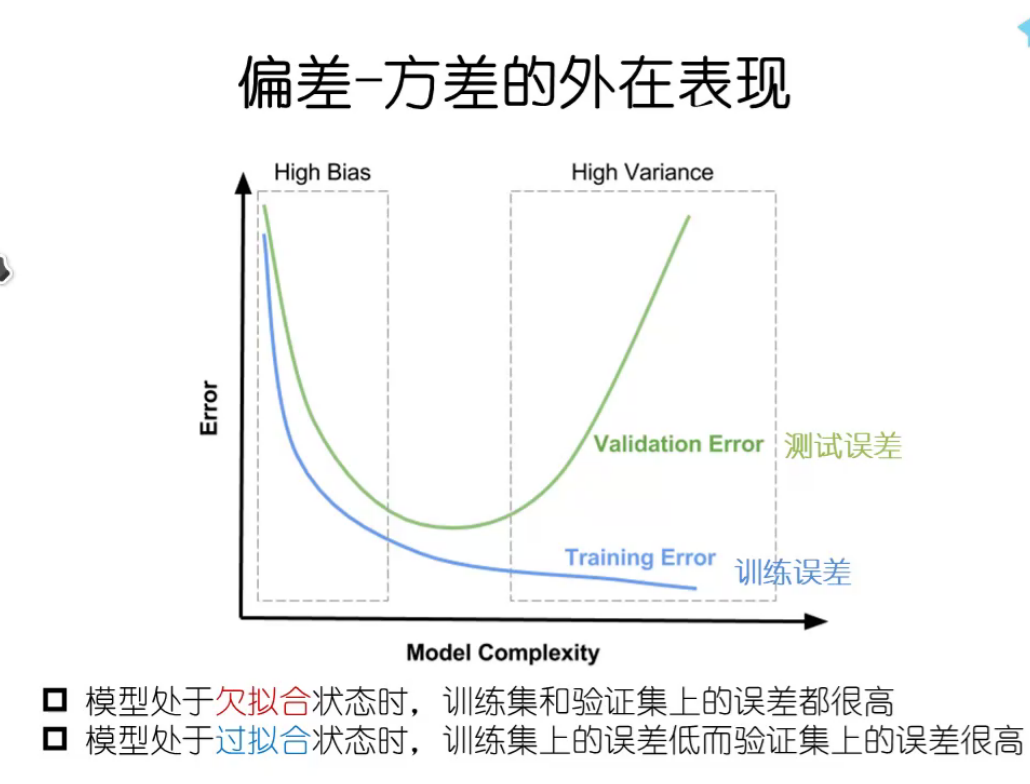
当模型高偏差时，加大训练集无用。

当模型高方差时，加大训练集可能有用。

大型神经网络比小型神经网络性能要好

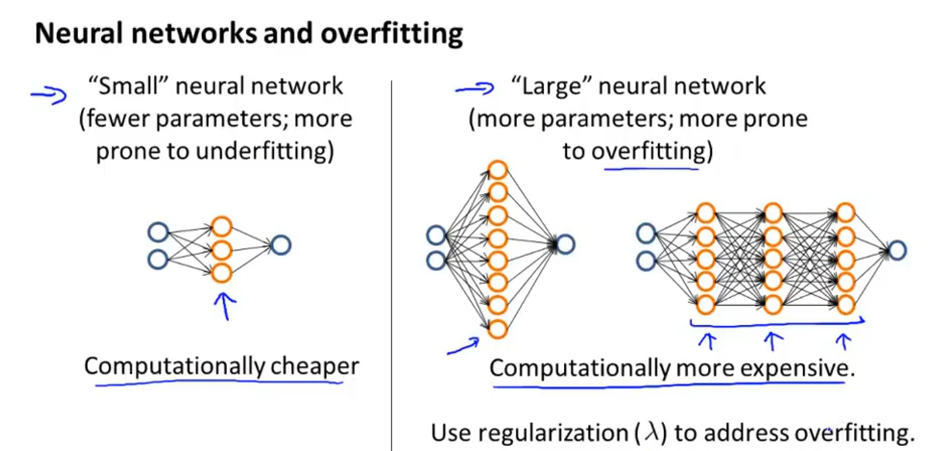
设计复杂学习系统

1. 从简单的算法开始
2. 绘制学习曲线
3. 误差分析（验证集）

误差评估

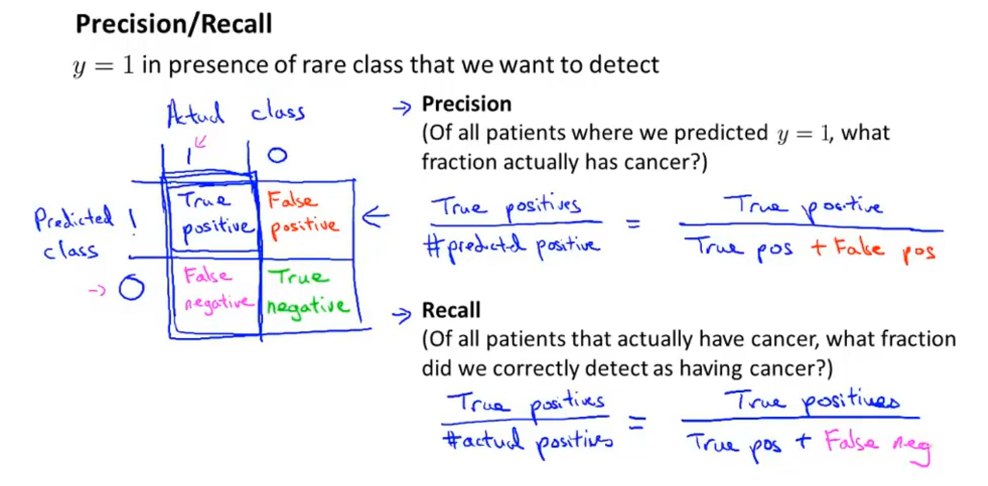
偏斜类 skewed class (其中一类占比巨大。不对称性分类)

查准率 = 真的 / 预测真的

召回率 = 真的 / （实际是真的，预测真或假）

平衡查准率与召回率

F_1的值

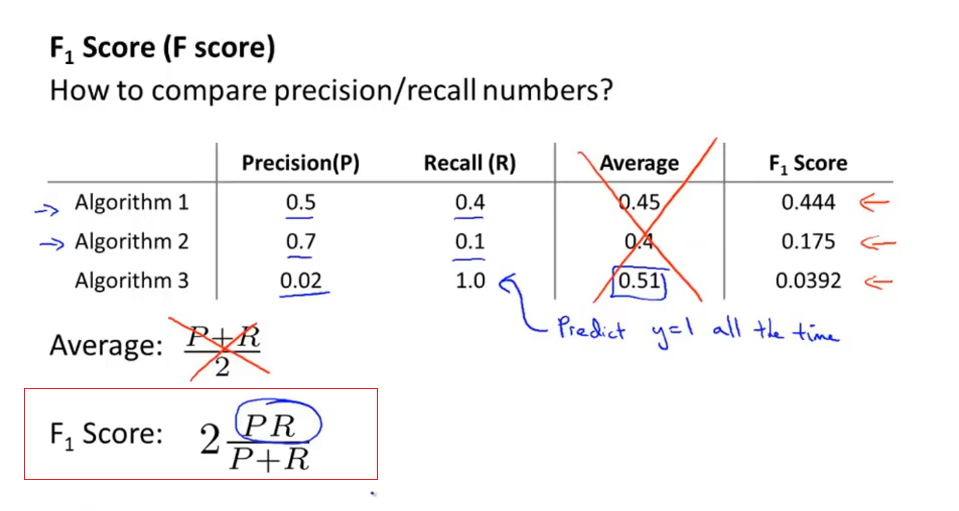
综合：

机器学习数据

大量数据 适合 大量参数的模型

编程作业

linearRegCostFunction.m

function [J, grad] = linearRegCostFunction(X, y, theta, lambda)
%LINEARREGCOSTFUNCTION Compute cost and gradient for regularized linear 
%regression with multiple variables
%   [J, grad] = LINEARREGCOSTFUNCTION(X, y, theta, lambda) computes the 
%   cost of using theta as the parameter for linear regression to fit the 
%   data points in X and y. Returns the cost in J and the gradient in grad

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;
grad = zeros(size(theta));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost and gradient of regularized linear 
%               regression for a particular choice of theta.
%
%               You should set J to the cost and grad to the gradient.
%


h = X * theta;
J = sum((h-y).^2)/2/m+ lambda/2/m*sum(theta(2:end).^2);
grad = X' * (h-y)/m + lambda/m*theta;
grad(1) = grad(1) - lambda/m*theta(1);

% =========================================================================

grad = grad(:);

end

learningCurve.m

function [error_train, error_val] = ...
    learningCurve(X, y, Xval, yval, lambda)
%LEARNINGCURVE Generates the train and cross validation set errors needed 
%to plot a learning curve
%   [error_train, error_val] = ...
%       LEARNINGCURVE(X, y, Xval, yval, lambda) returns the train and
%       cross validation set errors for a learning curve. In particular, 
%       it returns two vectors of the same length - error_train and 
%       error_val. Then, error_train(i) contains the training error for
%       i examples (and similarly for error_val(i)).
%
%   In this function, you will compute the train and test errors for
%   dataset sizes from 1 up to m. In practice, when working with larger
%   datasets, you might want to do this in larger intervals.
%

% Number of training examples
m = size(X, 1);

% You need to return these values correctly
error_train = zeros(m, 1);
error_val   = zeros(m, 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return training errors in 
%               error_train and the cross validation errors in error_val. 
%               i.e., error_train(i) and 
%               error_val(i) should give you the errors
%               obtained after training on i examples.
%
% Note: You should evaluate the training error on the first i training
%       examples (i.e., X(1:i, :) and y(1:i)).
%
%       For the cross-validation error, you should instead evaluate on
%       the _entire_ cross validation set (Xval and yval).
%
% Note: If you are using your cost function (linearRegCostFunction)
%       to compute the training and cross validation error, you should 
%       call the function with the lambda argument set to 0. 
%       Do note that you will still need to use lambda when running
%       the training to obtain the theta parameters.
%
% Hint: You can loop over the examples with the following:
%
%       for i = 1:m
%           % Compute train/cross validation errors using training examples 
%           % X(1:i, :) and y(1:i), storing the result in 
%           % error_train(i) and error_val(i)
%           ....
%           
%       end
%

% ---------------------- Sample Solution ----------------------

for i = 1:m   
      theta = trainLinearReg(X(1:i, :), y(1:i),lambda);
      error_train(i) = linearRegCostFunction(X(1:i, :), y(1:i),theta,0);
      error_val(i) = linearRegCostFunction(Xval, yval,theta,0);     
end

% -------------------------------------------------------------

% =========================================================================

end

polyFeatures.m

function [X_poly] = polyFeatures(X, p)
%POLYFEATURES Maps X (1D vector) into the p-th power
%   [X_poly] = POLYFEATURES(X, p) takes a data matrix X (size m x 1) and
%   maps each example into its polynomial features where
%   X_poly(i, :) = [X(i) X(i).^2 X(i).^3 ...  X(i).^p];
%


% You need to return the following variables correctly.
X_poly = zeros(numel(X), p);

% ====================== YOUR CODE HERE ======================
% Instructions: Given a vector X, return a matrix X_poly where the p-th 
%               column of X contains the values of X to the p-th power.
%
% 

for i = 1:numel(X)
  for j = 1:p
  X_poly(i,j) = X(i).^j;
endfor

% =========================================================================

end

validationCurve.m

function [lambda_vec, error_train, error_val] = ...
    validationCurve(X, y, Xval, yval)
%VALIDATIONCURVE Generate the train and validation errors needed to
%plot a validation curve that we can use to select lambda
%   [lambda_vec, error_train, error_val] = ...
%       VALIDATIONCURVE(X, y, Xval, yval) returns the train
%       and validation errors (in error_train, error_val)
%       for different values of lambda. You are given the training set (X,
%       y) and validation set (Xval, yval).
%

% Selected values of lambda (you should not change this)
lambda_vec = [0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]';

% You need to return these variables correctly.
error_train = zeros(length(lambda_vec), 1);
error_val = zeros(length(lambda_vec), 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return training errors in 
%               error_train and the validation errors in error_val. The 
%               vector lambda_vec contains the different lambda parameters 
%               to use for each calculation of the errors, i.e, 
%               error_train(i), and error_val(i) should give 
%               you the errors obtained after training with 
%               lambda = lambda_vec(i)
%
% Note: You can loop over lambda_vec with the following:
%
%       for i = 1:length(lambda_vec)
%           lambda = lambda_vec(i);
%           % Compute train / val errors when training linear 
%           % regression with regularization parameter lambda
%           % You should store the result in error_train(i)
%           % and error_val(i)
%           ....
%           
%       end
%
%

for i = 1:length(lambda_vec)
  lambda = lambda_vec(i);
  theta = trainLinearReg(X, y,lambda);
  error_train(i) = linearRegCostFunction(X, y,theta,0);
  error_val(i) = linearRegCostFunction(Xval, yval,theta,0);     
endfor


% =========================================================================

end