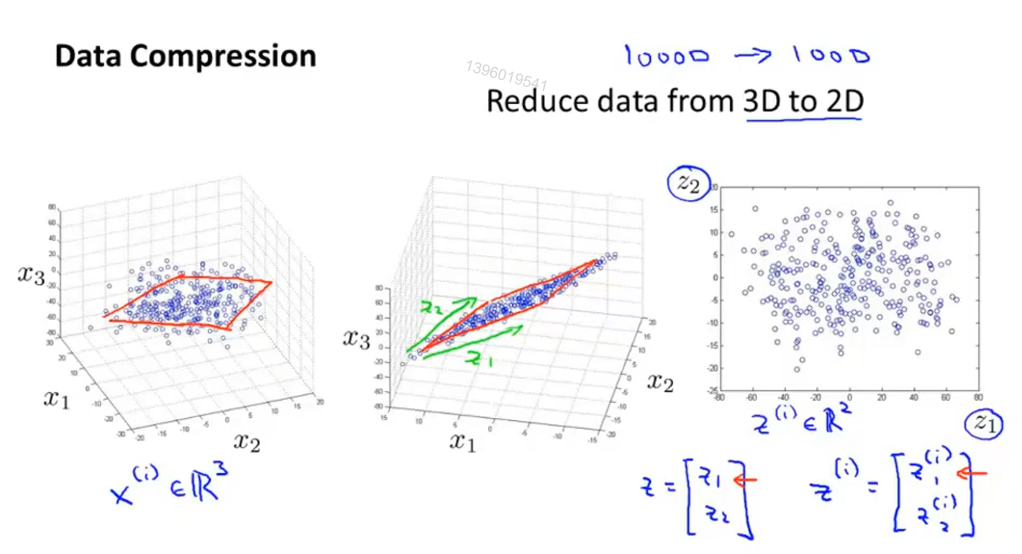
降维

运用于数据压缩,减少冗余

运用于可视化,抓住关键数据，绘制2D、3D图像

#

高维特征的问题：
• 存在大量冗余的特征，降低了机器学习的性能
• 数据可视化问题
• 数据处理的维度灾难
降维的目的：
• 发掘高维数据的内在维度，得到更紧凑(低维)的数据表达

机器学习最具有理论计算的部分，有点难

the Support Vector Machine (SVM)

监督学习算法

也称大间距分类器，因其设置了一个安全区域

在某些情况下比逻辑回归更适合构造非线性复杂分类器

模型选择

60% 训练集 20%验证集 20%测试集

训练集计算误差，利用交叉验证集选择维数，泛化能力

symbols

L ： 神经网络的层数

S_l ： 第 l 层神经网络的神经元数

K ：分类个数

代价函数

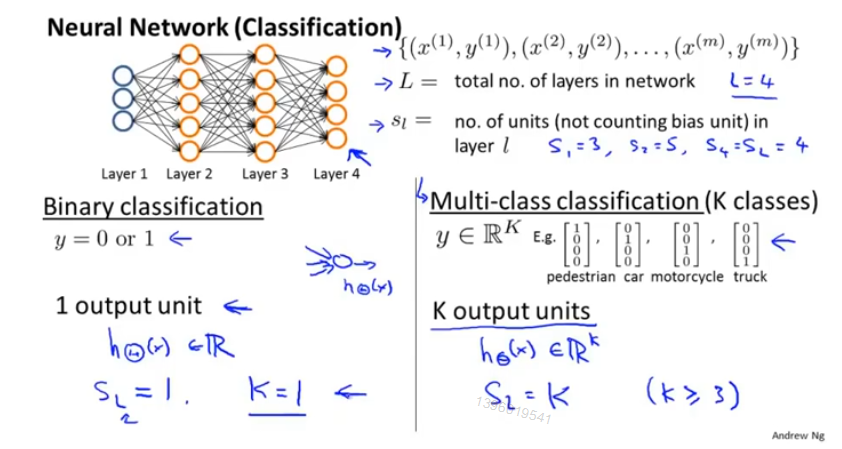
从逻辑回归算法中衍生到神经网络

每个 logistic regression algorithm 的代价函数 然后 K次输出 最后求和。

不对偏置单元(bias)进行正则化操作，即含X_0的项

原因

适应于非线性假设

sigmoid（logistic）activation function : 激活函数 指代 g(z)

X_0 偏置单元，值永远是1

θ 代表 参数或权重

架构

输入层-》隐藏层（不止一个）-》输出层

符号：

a(i)_j表示 第i层，第j个神经元或单元的激活项(由具体的神经元计算并输出的值)

θ(i) 表示 从第i层到第i+1层之间映射的权重矩阵

偏置单元省略没有写。

sigmoid function also logistic function

“分类问题”–逻辑回归算法

决策边界 不是训练集的属性，而是假设本身和其参数的属性

计算的是 属于1 的概率

分类

监督学习 supervised learning

“right answer” for each of our examples in the data

regression(回归) ：predict a real-valued output

classification(分类)：predict discrete-valued output (类似于0、1问题)

无监督学习 unsupervise learning

数据未标记，类别未知。

计算机自己根据样本间的相似性对样本集进行分类

单变量线性回归

symbols

m = number of training examples

x’s = “input” variable / features

y’s = “output”variable / “target” variable

(x,y) - one training example

(x^(i) , y^(i)) - the i training example ( i 表示索引，不是幂)

hypothesis（假设，机器学习术语— 输出函数）

univariate 单因素

代价函数

调整参数 最小化代价函数—– h(x)-y ，拟合数据